题目内容
8.已知4x2+y2-4x-6y+10=0,求($\frac{2}{3}$x$\sqrt{9x}$+y2$\sqrt{\frac{x}{{y}^{2}}}$)-(x2$\sqrt{\frac{1}{x}}$-5x$\sqrt{\frac{y}{x}}$)的值.分析 先利用配方法得到(2x-1)2+(y-3)2=0,再利用非负数的性质得x=$\frac{1}{2}$,y=3,接着把原式中的各二次根式化为最简二次根式,然后合并后把x和y的值代入计算即可.
解答 解:∵4x2+y2-4x-6y+10=0,
∴4x2-4x+1+y2-6y+9=0,
∴(2x-1)2+(y-3)2=0,
∴2x-1=0,y-3=0,
∴x=$\frac{1}{2}$,y=3,
原式=2x$\sqrt{x}$+y$\sqrt{x}$-x$\sqrt{x}$+5$\sqrt{xy}$
=(x+y)$\sqrt{x}$+5$\sqrt{xy}$,
当x=$\frac{1}{2}$,y=3时,原式=($\frac{1}{2}$+3)×$\sqrt{\frac{1}{2}}$+5×$\sqrt{\frac{1}{2}×3}$
=$\frac{7\sqrt{2}}{4}$+$\frac{5\sqrt{6}}{2}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.也考查了非负数的性质.

练习册系列答案
相关题目
16.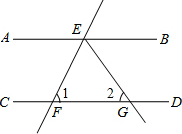 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
 如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )
如图,已知AB∥CD,直线EF分别交 AB、CD于点E,F,EG平分∠BEF交CD于点G.如果∠1=70°,那么∠2的度数是( )| A. | 70° | B. | 65° | C. | 55° | D. | 22.5° |
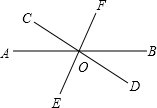 如图,直线AB、CD、EF相交于点O,∠AOC=35°,∠COF=80°.
如图,直线AB、CD、EF相交于点O,∠AOC=35°,∠COF=80°.