题目内容
4.4个数a,b,c,d排列成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,我们称之为二阶行列式.规定它的运算法则为:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.若$|\begin{array}{l}{x+3}&{x-3}\\{x-3}&{x+3}\end{array}|$=12,则x=1.分析 利用题中的新定义化简已知等式,求出解即可得到x的值.
解答 解:利用题中新定义得:(x+3)2-(x-3)2=12,
整理得:12x=12,
解得:x=1.
故答案为:1.
点评 此题考查了整式的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
14.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为( )
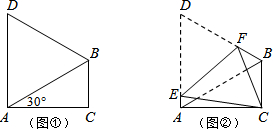

| A. | $\frac{\sqrt{3}-1}{7}$ | B. | $\frac{1}{7}$ | C. | $\frac{\sqrt{3}}{12}$ | D. | $\frac{\sqrt{3}-1}{6}$ |
12.如图1所示,?ABCD中,动点P从点B出发,沿BC,CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的图象如图2所示,则?ABCD的面积是( )
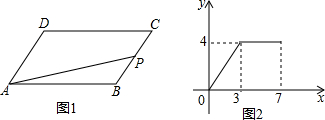

| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
19.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-6),则k的值为( )
| A. | -12 | B. | 12 | C. | -3 | D. | 3 |
9.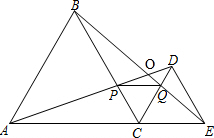 如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:
如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:
①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
其中正确的有( )
 如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:
如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,则有以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
其中正确的有( )
| A. | ①③⑤ | B. | ①③④⑤ | C. | ①②③⑤ | D. | ①②③④⑤ |
13.某公司招聘人才,对应聘者分别进行阅读能力,思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
| 项目 人员 | 阅读 | 思维 | 表达 |
| 甲 | 93 | 86 | 73 |
| 乙 | 95 | 81 | 79 |
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
14.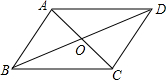 ?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
 ?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )| A. | 61° | B. | 63° | C. | 65° | D. | 67° |
