题目内容
6. 如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.
如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.(1)求tan∠ABE的值.
(2)求$\frac{{S}_{△BEF}}{{S}_{正方形ABCD}}$的值.
分析 (1)根据三角形的重心的性质得到CP=2OP,根据平行线分线段成比例定理、正切的概念计算即可;
(2)设正方形的边长为a,求出EF、BP,根据三角形的面积公式计算即可.
解答 解:(1)∵点O是△BEF的重心,
∴OB=2OP,
则点P是OC的中点,
∵EF∥AD,
∴点E是AD的中点,
∴tan∠ABE=$\frac{AE}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$;
(2)设正方形的边长为a,
则BC=$\sqrt{2}$a,
∴EF=$\frac{1}{2}$AD=$\frac{\sqrt{2}}{2}$a,BP=$\frac{3\sqrt{2}}{4}$a,
∴$\frac{{S}_{△BEF}}{{S}_{正方形ABCD}}$=$\frac{\frac{1}{2}×\frac{\sqrt{2}}{2}a×\frac{3\sqrt{2}}{2}a}{{a}^{2}}$×$\frac{1}{2}$=$\frac{3}{8}$.
点评 本题考查的是三角形的重心的概念和性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
相关题目
18.计算(-1)2-(-1)3=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
10.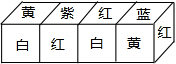 把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
现将上述大小相同,颜色、花朵分布完全一样的四个正方体拼成一个在同一平面上放置的长方体,如图所示,那么长方体的下底面共有17朵花.
 把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:
把正方体的6个面分别涂上不同的颜色,并画上朵数不等的花,各面上的颜色与花朵数的情况如下表:| 颜色 | 红 | 黄 | 蓝 | 白 | 紫 | 绿 |
| 花朵数 | 1 | 2 | 3 | 4 | 5 | 6 |
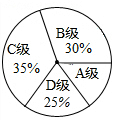 为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.
为了解某区3600名九年级学生的体育训练情况,随机抽取了区内200名九年级学生进行了一次体育模拟测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如图所示的统计图,由此估计全区九年级体育测试成绩可以达到优秀的人数约为360人.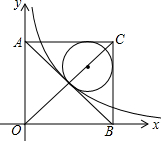 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.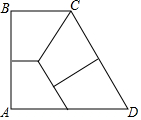 如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC=$\sqrt{3}$:1.
如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC=$\sqrt{3}$:1.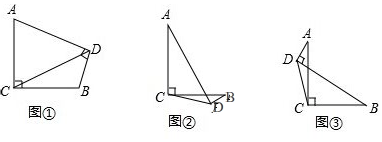
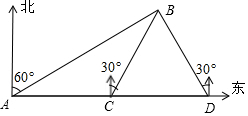 如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.
如图,某货轮上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到到达C,D处的时间.