题目内容
12. 如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
如图,一次函数y=x+b的图象过点A(1,2),且与x轴相交于点B,若点P是x轴上的一点,且满足△APB是等腰三角形,则点P的坐标可以是(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
分析 先把点A(1,2)代入一次函数y=x+b求出b的值,故可得出B点坐标,再分AB=AP,AB=BP及AP=BP三种情况进行分类讨论.
解答 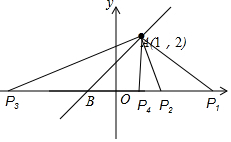 解:∵一次函数y=x+b的图象过点A(1,2),
解:∵一次函数y=x+b的图象过点A(1,2),
∴2=1+b,解得b=1,
∴一次函数的解析式为:y=x+1,
∴B(-1,0).
当AB=AP时,
∵B(-1,0),
∴P1(3,0);
当AB=BP时,
∵AB=$\sqrt{{(1+1)}^{2}+(2-0)^{2}}$=2$\sqrt{2}$,
∴P1(2$\sqrt{2}$-1,0),P3(-2$\sqrt{2}$-1,0);
当AP=BP时,点P在线段AB的垂直平分线上,线段AB的中点坐标为(0,1),
设点P所在的直线解析式为y=-x+c,则c=1,
∴直线解析式为y=-x+1,
∴当y=0时,x=1,
∴P4(1,0).
综上所述,P点坐标为:(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
故答案为:(3,0),(2$\sqrt{2}$-1,0),(-2$\sqrt{2}$-1,0),(1,0).
点评 本题考查的是一次函数图象上点的坐标特点,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
2. 如图所示,△ABC中,DE∥BC,AC=9,CE=6,AD=4,则BD的值为( )
如图所示,△ABC中,DE∥BC,AC=9,CE=6,AD=4,则BD的值为( )
 如图所示,△ABC中,DE∥BC,AC=9,CE=6,AD=4,则BD的值为( )
如图所示,△ABC中,DE∥BC,AC=9,CE=6,AD=4,则BD的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
3. 如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
 如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )
如图,在△ABC中,D,E分别是边AB,AC上的点,且DE∥BC,F、G在BC上,DG∥AC,EF∥AB,DG与EF相交于点H,若S△FHG=1,S△HDE=9,则△ABC的面积为( )| A. | 100 | B. | 81 | C. | 64 | D. | 49 |
20. 将一副三角板如图方式放置,则∠1的度数是( )
将一副三角板如图方式放置,则∠1的度数是( )
 将一副三角板如图方式放置,则∠1的度数是( )
将一副三角板如图方式放置,则∠1的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
4.据统计,2017年春节黄金周7天,杭州共接待中外游客约450万人次,将450万用科学记数法表示,以下表示正确的是( )
| A. | 450×104 | B. | 45.0×105 | C. | 4.50×106 | D. | 4.50×107 |
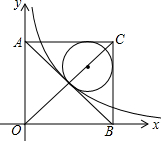 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.