题目内容
15.若x<0,y>0,求$\frac{|x|}{x}$+$\frac{|y|}{y}$+$\frac{|xy|}{xy}$的值.分析 先计算绝对值,再计算除法,最后相减即可求解.
解答 解:∵x<0,y>0,
∴$\frac{|x|}{x}$+$\frac{|y|}{y}$+$\frac{|xy|}{xy}$
=$\frac{-x}{x}$+$\frac{y}{y}$+$\frac{-xy}{xy}$
=-1+1-1
=-1.
点评 考查了有理数的乘除法,绝对值,关键是熟练掌握绝对值的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.若|a|=2,b的相反数是最大的负整数,c是绝对值最小的数,则-a+b-c的值为( )
| A. | 0 | B. | 3或-1 | C. | 2 | D. | -1 |
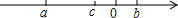 已知有理数a,b,c在数轴上的位置如图所示:化简$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$.
已知有理数a,b,c在数轴上的位置如图所示:化简$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$.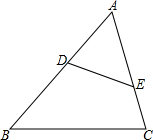 已知:如图,在△ABC中,点D、E分别在AB、AC上,且∠AED=∠B.
已知:如图,在△ABC中,点D、E分别在AB、AC上,且∠AED=∠B.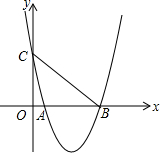 如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点,最低点的纵坐标为-4,与y轴交于点C.
如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点,最低点的纵坐标为-4,与y轴交于点C.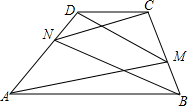 如图,梯形ABCD中AB∥CD,AB>CD,N、M分别是腰AD、CB上的点,已知∠DAM=∠CBN.求证:∠DMA=∠CNB.
如图,梯形ABCD中AB∥CD,AB>CD,N、M分别是腰AD、CB上的点,已知∠DAM=∠CBN.求证:∠DMA=∠CNB.