题目内容
3.已知$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{2}{3}$,求$\frac{2a-c-5e}{2b-d-5f}$的值.分析 根据比例的性质,可用b表示a,用d表示c,用f表示e,根据等式的性质,可得答案.
解答 解:由$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{2}{3}$,得
a=$\frac{2}{3}$b,c=$\frac{2}{3}$d,e=$\frac{2}{3}$f.
$\frac{2a-c-5e}{2b-d-5f}$=$\frac{\frac{4}{3}b-\frac{2}{3}d-\frac{10}{3}f}{2b-d-5f}$=$\frac{\frac{2}{3}(2b-d-5f)}{2b-d-5f}$=$\frac{2}{3}$.
点评 本题考查了比例的性质,利用比例的性质得出b表示a,用d表示c,用f表示e是解题关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
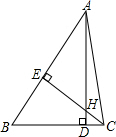 如图所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于H,若AE=CE,求证:△AEH≌△CEB.
如图所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE相交于H,若AE=CE,求证:△AEH≌△CEB.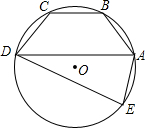 如图,在⊙O上依次有点A、B、C、D、E,且AB=BC=CD.若∠BAD=50°,则∠AED=75°.
如图,在⊙O上依次有点A、B、C、D、E,且AB=BC=CD.若∠BAD=50°,则∠AED=75°.