Question

10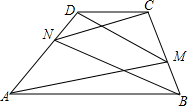．如图，梯形ABCD中AB∥CD，AB＞CD，N、M分别是腰AD、CB上的点，已知∠DAM=∠CBN．求证：∠DMA=∠CNB．

Answer 1

分析 连接MN，由∠DAM=∠CBN，得到A，B，M，N四点共圆，得出∠DAB=∠CMN，∠ANB=∠AMB，由梯形的性质得出∠DAB+∠ADC=180°，得到∠CMN+∠ADC=180°，因此C，D，N，M四点共圆，由圆周角定理得出∠CMD=∠DNC，即可得到∠DMA=∠CNB．

解答 证明：连接MN，如图所示：
∵∠DAM=∠CBN，
∴A，B，M，N四点共圆，
∴∠DAB=∠CMN，∠ANB=∠AMB，
又∵AB∥DC，
∴∠DAB+∠ADC=180°，
∴∠CMN+∠ADC=180°．
∴C，D，N，M四点共圆，
∴∠CMD=∠DNC，
∴180°-∠DNC-∠ANB=180°-∠CMD-∠AMB，
∴∠DMA=∠CNB．

点评 本题是四点共圆题目，考查了四点共圆、圆周角定理、圆内接四边形的性质、梯形的性质等知识；本题综合性强，有一定难度，通过作辅助线两次证明四点共圆，运用圆周角定理得出角之间的关系才能得出结论．