题目内容
8．
如图，△ABC中，∠BAC=120°，AB=AC，AD⊥BC，垂足为D，则∠BAD的度数是60°．
分析 直接根据等腰三角形三线合一的性质即可得出结论．
解答 解：∵△ABC中，∠BAC=120°，AB=AC，AD⊥BC，
∴AD是∠BAC的平分线，
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×120°=60°．
故答案为：60°．
点评 本题考查的是等腰三角形的性质，熟知等腰三角形“三线合一”的性质是解答此题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠C=90°，∠A=30°，BC=$\sqrt{3}$，求AC的长．
16．某种签字笔的单价为2元，购买这种签字笔x支的总价为y元．则y与x之间的函数关系式为（ ）
| A． | y=-$\frac{1}{2}$x | B． | y=$\frac{1}{2}$x | C． | y=-2x | D． | y=2x |
20．已知关于x的方程5（x-a）=-2a的根大于关于x的方程3（x-a）=2（x+a）的根，则a应是（ ）
| A． | 不为0的数 | B． | 正数 | C． | 负数 | D． | 大于-1的数 |
12．
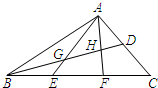如图，在△ABC中，AD=DC，BE=EF=FC，AE、AF与BD相交于点G、H．已知${S_{△AHD}}=\frac{3}{10}$，则S四边形GEFH的值是（ ）
如图，在△ABC中，AD=DC，BE=EF=FC，AE、AF与BD相交于点G、H．已知${S_{△AHD}}=\frac{3}{10}$，则S四边形GEFH的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{7}{10}$ | C． | $\frac{6}{11}$ | D． | $\frac{11}{20}$ |
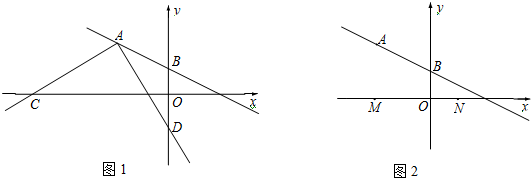
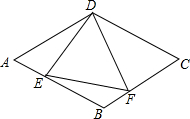如图，菱形ABCD中，AB=6，∠A=60°，点E是线段AB上一点（不与A，B重合），作∠EDF交BC于点F，且∠EDF=60°．