题目内容
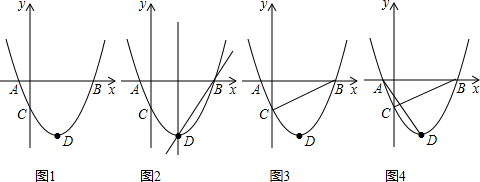
3. 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先根据二次函数图象开口方向可得a>0,根据图象与y轴交点可得c<0,再根据二次函数的对称轴x=-$\frac{b}{2a}$,结合图象与x轴的交点可得对称轴为x=1,根据对称轴公式结合a的取值可判定出b<0进而解答即可.
解答 解:根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
故①ac<0正确;
对称轴:x=-$\frac{b}{2a}$>0,
∵它与x轴的两个交点分别为(-1,0),(3,0),
∴对称轴是x=1,
∴-$\frac{b}{2a}$=1,
∴b+2a=0,
故②2a+b=0正确;
把x=2代入y=ax2+bx+c=4a+2b+c,由图象可得4a+2b+c<0,
故③4a+2b+c>0错误;
∵抛物线的对称轴为直线x=1,∴当x=1时,y的最小值为a+b+c,∴对于任意x均有ax2+bx≥a+b,
故④正确;
故选C
点评 此题主要考查了二次函数图象与系数的关系,关键是熟练掌握①二次项系数a决定抛物线的开口方向,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c).

练习册系列答案
相关题目
13.要调查下面的问题,其中最合适普查的是( )
| A. | 调查某种灯泡的使用寿命 | B. | 调查你所在的班级学生的体重情况 | ||
| C. | 调查我国七年级学生的视力情况 | D. | 调查CCTV某档电视节目的收视情况 |
15.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )
| A. | (-4,2) | B. | (4,-2) | C. | (2,4) | D. | (-2,-4) |
 宝应运河大桥横跨京杭大运河,是连接宝应县城区与运西的重要通道,该桥原先坐落于扬州,1985年,当时的江苏省交通部门决定,将重达668吨的此桥,从扬州整体走水路浮运到108公里外的宝应安装使用,这成为我国桥梁史上的创举.运河大桥是宝应的一个标志性建筑,其拱形图形为呈圆弧形,其最高点C离桥面AB的高CD=4m,弦AB=60m,求桥拱所在的半径.
宝应运河大桥横跨京杭大运河,是连接宝应县城区与运西的重要通道,该桥原先坐落于扬州,1985年,当时的江苏省交通部门决定,将重达668吨的此桥,从扬州整体走水路浮运到108公里外的宝应安装使用,这成为我国桥梁史上的创举.运河大桥是宝应的一个标志性建筑,其拱形图形为呈圆弧形,其最高点C离桥面AB的高CD=4m,弦AB=60m,求桥拱所在的半径. (1)在直角坐标系中画出顶点坐标分别为:A(4,-1),B(3,-5),C(1,-3)的三角形△ABC.
(1)在直角坐标系中画出顶点坐标分别为:A(4,-1),B(3,-5),C(1,-3)的三角形△ABC.
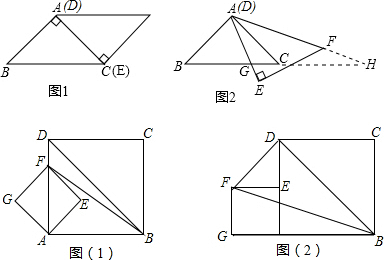
 用无刻度的直尺画一条直线将图?①、图?②分成面积相等的两部分(保留作图痕迹)
用无刻度的直尺画一条直线将图?①、图?②分成面积相等的两部分(保留作图痕迹)