题目内容
16.△ABC中,a、b、c分别为∠A、∠B、∠C的对边,且关于x的方程2ax2+2cx+b=0有两个实数根.(1)若∠C=90°,方程有两个相等的实数根,求a:b:c的值;
(2)若∠A=∠B,方程两根为x1、x2,且x1-x2=1,求∠C的度数.
分析 (1)根据勾股定理结合根的判别式可得出关于a、b、c的三元二次方程组,解方程组用a表示出b和c,由此即可得出结论;
(2)由∠A=∠B即可得出a=b,结合根与系数的关系即可找出x1+x2=-$\frac{c}{a}$、x1•x2=$\frac{b}{2a}$=$\frac{1}{2}$,联立x1-x2=1即可求出c与a之间的关系,再通过解直角三角形可得出$\frac{1}{2}$∠C的度数,此题得解.
解答 解:(1)根据题意,得:$\left\{\begin{array}{l}{{c}^{2}={a}^{2}+{b}^{2}}\\{△=4{c}^{2}-8ab=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=a}\\{c=\sqrt{2}a}\end{array}\right.$,
∴a:b:c=1:1:$\sqrt{2}$.
(2)∵∠A=∠B,
∴a=b.
∵x1+x2=-$\frac{c}{a}$,x1•x2=$\frac{b}{2a}$=$\frac{1}{2}$,且x1-x2=1,
∴$({x}_{1}+{x}_{2})^{2}$=$({x}_{1}-{x}_{2})^{2}$+4x1•x2,即$\frac{{c}^{2}}{{a}^{2}}$=1+2=3,
∴c=$\sqrt{3}$a.
sin$\frac{1}{2}$∠C=$\frac{\frac{c}{2}}{a}$=$\frac{\frac{\sqrt{3}}{2}a}{a}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{1}{2}$∠C=60°,
∴∠C=120°.
点评 本题考查了根与系数的关系、根的判别式以及解直角三角形,通过解方程组找出a、b、c间的关系是解题的关键.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | ±7 | B. | ±11 | C. | -7或11 | D. | -7或-11 |
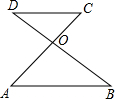 如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.
如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.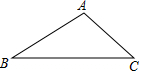 已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.
已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.