题目内容
 已知四边形ABCD中,AB∥CD,AC=CD,AD=OD,∠BCA=15°.求证:△CBD为等腰直角三角形.
已知四边形ABCD中,AB∥CD,AC=CD,AD=OD,∠BCA=15°.求证:△CBD为等腰直角三角形.考点:梯形,等腰直角三角形
专题:证明题
分析:先根据等边对等角得到角的关系,进而推出∠ODA的度数,然后即可得到结论.
解答:证明:∵AB∥CD,AC=CD,AD=OD,∠BCA=15°,
∴∠BAC=∠ACD,∠BACD+∠CDA=180°,∠CAD=∠CDA,∠DAO=∠DOA,
∵∠ODA+∠ODC=
(180°-∠ODA),∠BOA=∠ODA+∠OAD,
∴∠ODA=30°,
∴∠BDC=∠BCD=45°,
∴△BCD为等腰直角三角形.
∴∠BAC=∠ACD,∠BACD+∠CDA=180°,∠CAD=∠CDA,∠DAO=∠DOA,
∵∠ODA+∠ODC=
| 1 |
| 2 |
∴∠ODA=30°,
∴∠BDC=∠BCD=45°,
∴△BCD为等腰直角三角形.
点评:该题目考查了等腰三角形的性质,关键是求出∠ODA的度数.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
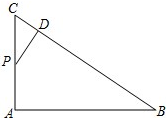 如图,在Rt△ABC中,∠A=90°,P是AC中点,PD⊥BC,D为垂足,BC=9,CD=3.求AB2的值.
如图,在Rt△ABC中,∠A=90°,P是AC中点,PD⊥BC,D为垂足,BC=9,CD=3.求AB2的值.
 如图,已知二次函数的顶点坐标为D(-1,-8),与y轴交于点C(0,-6),与x轴交于A、B两点,求△ABC的面积.
如图,已知二次函数的顶点坐标为D(-1,-8),与y轴交于点C(0,-6),与x轴交于A、B两点,求△ABC的面积. 正方形ABCD中,E是BC延长线上的点,BF⊥DE于F,连接AF,探究线段AF、BF、DF的数量关系.
正方形ABCD中,E是BC延长线上的点,BF⊥DE于F,连接AF,探究线段AF、BF、DF的数量关系.