题目内容
如图，在⊙O的内接四边形ABCD中，∠BAD=60°，∠ACB=70°．求∠BCD和∠ABD的度数．考点：圆周角定理,圆内接四边形的性质
专题：
分析：先由圆内接四边形的对角互补得出∠BCD=180°-∠BAD=120°，再由∠ACB=70°得到∠ACD=50°，然后根据圆周角定理即可得出∠ABD=∠ACD=50°．
解答：解：∵在⊙O的内接四边形ABCD中，∠BAD=60°，
∴∠BCD=180°-∠BAD=120°，
∵∠ACB=70°，
∴∠ACD=∠BCD-∠ACB=50°，
∴∠ABD=∠ACD=50°．
∴∠BCD=180°-∠BAD=120°，
∵∠ACB=70°，
∴∠ACD=∠BCD-∠ACB=50°，
∴∠ABD=∠ACD=50°．
点评：本题考查了圆内接四边形的性质，圆周角定理，难度适中．准确求出∠BCD的度数是解题的关键．
练习册系列答案
字词句段篇系列答案
相关题目
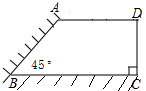校园要建苗圃，其形状如直角梯形，有两边借用夹角为45°的两面墙，如图，另外两边是总长为30m的铁栅栏．
如图，已知二次函数的顶点坐标为D（-1，-8），与y轴交于点C（0，-6），与x轴交于A、B两点，求△ABC的面积．
如图所示，在四边形ACBM中，已知MB=2MA，MC=BC，∠1=∠2，求证：MA⊥AC．
正方形ABCD中，E是BC延长线上的点，BF⊥DE于F，连接AF，探究线段AF、BF、DF的数量关系．