题目内容
17.如图,已知抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,3)三点.(1)求抛物线相应的函数表达式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,连接NB.若点M的横坐标为t,是否存在t,使MN的长最大?若存在,求出sin∠MBN的值;若不存在,请说明理由;
(3)若对一切x≥0均有ax2+bx+c≤mx-m+13成立,求实数m的取值范围.
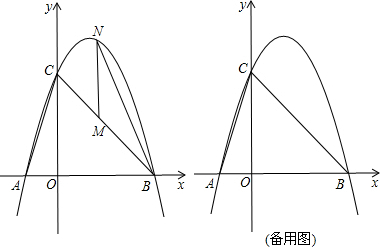
分析 (1)用待定系数法即可求出抛物线的解析式;
(2)先求出直线BC的解析式,设M(t,-t+3),N(t,-t2+2t+3),得出MN是t的二次函数,即可求出MN的最大值;延长NM交OB于E,证出△BME为等腰直角三角形,求出BE、BM、BN,过点M作△BNM的高MH,则∠MHB=∠MHN=90°,设BH=x,根据勾股定理求出BH,再由勾股定理求出MH,即可求出sin∠MBN;
(3)令y1=-x2+2x+3;y2=mx-m+13,得直线y2=mx-m+13过点(1,13);当y1=y2时,-x2+2x+3=mx-m+13,得出△=m2-36=0,求出m的值,当直线y2=mx-m+13过点C时,m=10,结合图象即可得出m的取值范围.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a-b+c=0}&{\;}\\{9a+3b+c=0}&{\;}\\{c=3}&{\;}\end{array}\right.$,
解得:a=-1,b=2,c=3,
∴抛物线的函数表达式为:y=-x2+2x+3;
(2)存在;理由如下:设直线BC的解析式为y=kx+b,
把B(3,0)、C(0,3)代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:k=-1,b=3,
∴直线BC的解析式为:y=-x+3,
设M(t,-t+3),N(t,-t2+2t+3),
则MN=(-t2+2t+3)-(-t+3)=-t2+3t=-(t-$\frac{3}{2}$)2+$\frac{9}{4}$;
∵-1<0,
∴MN由最大值,
当t=$\frac{3}{2}$时,MN的最大值为$\frac{9}{4}$;
此时M($\frac{3}{2}$,$\frac{3}{2}$),N($\frac{3}{2}$,$\frac{15}{4}$),
∴MN=$\frac{15}{4}$-$\frac{3}{2}$=$\frac{9}{4}$,
∵B(3,0)、C(0,3),
∴OB=OC=3,
∵∠BOC=90°,
∴∠OBC=45°,
延长NM交OB于E,如图1所示: 则ME⊥OB,
则ME⊥OB,
∴△BME为等腰直角三角形,
∴∠MBE=45°,
∵BE=3-$\frac{3}{2}$=$\frac{3}{2}$,
∴BM=$\sqrt{2}$BE=$\frac{3\sqrt{2}}{2}$;
BN=$\sqrt{B{E}^{2}+N{E}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+(\frac{15}{4})^{2}}$=$\frac{3\sqrt{29}}{4}$;
过点M作△BNM的高MH,则∠MHB=∠MHN=90°,
∵MH2=BM2-BH2=MN2-NH2,
设BH=x,则NH=$\frac{3\sqrt{29}}{4}$-x,
∴($\frac{3\sqrt{2}}{2}$)2-x2=($\frac{9}{4}$)2-($\frac{3\sqrt{29}}{4}$-x)2,
解得:x=$\frac{21\sqrt{29}}{58}$,
∴BH=$\frac{21\sqrt{29}}{58}$,
∴MH=$\sqrt{(\frac{3\sqrt{2}}{2})^{2}-(\frac{21\sqrt{29}}{58})^{2}}$=$\frac{9\sqrt{29}}{58}$;
∴sin∠MBN=$\frac{MH}{BM}$=$\frac{3\sqrt{58}}{58}$;
(3)令y1=-x2+2x+3; y2=mx-m+13,
∵x=1时,y2=13,
∴直线y2=mx-m+13过点(1,13),
当y1=y2时,-x2+2x+3=mx-m+13,
整理得:x2+(m-2)x-m+10=0,
△=(m-2)2-4×1×(-m+10)=m2-36=0,
解得:m=-6,或m=6,
当直线y2=mx-m+13过点C时,m=10,
由图象可知(如图2所示),
当-6≤m≤10时,均有y1≤y2,
∴m的取值范围为:-6≤m≤10.
点评 本题是二次函数综合题目,考查了用待定系数法求二次函数的解析式、求一次函数的解析式、等腰直角三角形的判定与性质、勾股定理、三角函数等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线证明等腰直角三角形和运用勾股定理才能得出结果.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |

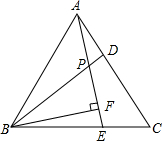 如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.
如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.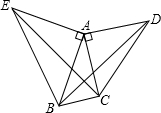 如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问:
如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,∠BAC=30°,若△EAC绕某点逆时针旋转后能与△BAD重合,问: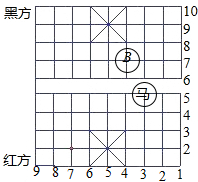 观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).
观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).