题目内容
9.先化简,再求值:$\frac{a-3}{3{a}^{2}-6a}$÷($\frac{5}{a-2}$-a-2),其中a2+3a-1=0.分析 先把括号内通分,再把分子分母因式分解,接着把除法运算化为乘法运算,则约分后得到原式=-$\frac{1}{3{a}^{2}+3a}$,然后把a2+3a-1=0变形得到a2+3a=1,再利用整体代入的方法计算.
解答 解:原式=$\frac{a-3}{3a(a-2)}$÷$\frac{5-(a+2)(a-2)}{a-2}$
=$\frac{a-3}{3a(a-2)}$•$\frac{a-2}{-(a+3)(a-3)}$
=-$\frac{1}{3a(a+3)}$
=-$\frac{1}{3{a}^{2}+3a}$,
∵a2+3a-1=0,
∴a2+3a=1,
∴原式=-$\frac{1}{3×1}$=-$\frac{1}{3}$.
点评 分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
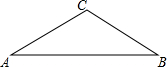 如图,已知在等腰△ABC中,∠C=120°
如图,已知在等腰△ABC中,∠C=120°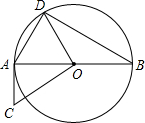 如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,
如图,AB是⊙O的直径,CA与⊙O相切于点A,点D在⊙O上,且OD⊥OC,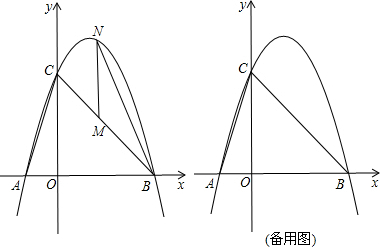
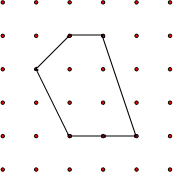 各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6
各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+$\frac{1}{2}$b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+$\frac{1}{2}$×6-1=6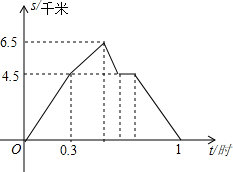 从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )
从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )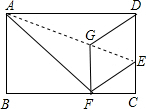 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.