题目内容
2.若kb>0,且不等式kx+b>0的解集是x<-$\frac{b}{k}$,则下列判断正确的是( )| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
分析 首先根据不等式kx+b>0的解集是x<-$\frac{b}{k}$,应用不等式的性质,可得k<0;然后根据kb>0,可得b<0,据此解答即可.
解答 解:∵不等式kx+b>0的解集是x<-$\frac{b}{k}$,
∴k<0,
又∵kb>0,
∴b<0,
综上,可得k<0,b<0.
故选:C.
点评 此题主要考查了不等式的解集问题,要熟练掌握,解答此题的关键是根据不等式的性质,判断出k<0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.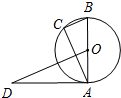 如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )
 如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )
如图,AB是⊙O的直径,AD是⊙O的切线,BC∥OD交⊙O于点C,若AB=2,OD=3,则BC的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
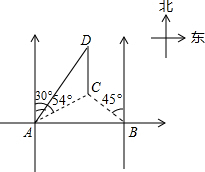 如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)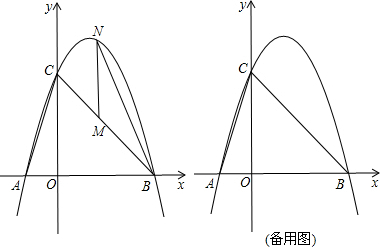
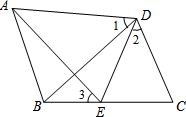 已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.
已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.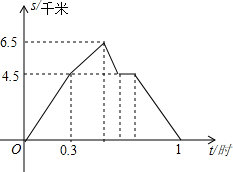 从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )
从A到B地的一条公路,先是一段平路,然后是一段上坡路,小明骑自行车从A地出发,到达B地后立即按原路返回A地,返回途中休息了一段时间,假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进.已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米.下坡路的速度比在平路上的速度每小时多5千米,小明在去B地和返回A地两次经过C地的时间间隔为0.15小时,小明离A地的路程S(单位:千米)和出发的时间t(单位:小时)之间的函数关系式如图所示.下列说法中正确的个数为( )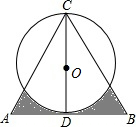 如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π).
如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为2.5$\sqrt{3}$-π(结果保留π). 平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=24°.
平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1-∠2=24°.