题目内容
6．已知关于x的不等式（1-a）x＞-6的解集为x＜$\frac{6}{a-1}$，则a的取值范围是a＞1．分析 首先根据不等式（1-a）x＞-6的解集为x＜$\frac{6}{a-1}$，应用不等式的性质，可得1-a＜0；然后解一元一次不等式，求出a的取值范围即可．
解答 解：∵不等式（1-a）x＞-6的解集为x＜$\frac{6}{a-1}$，
∴1-a＜0，
∴a＞1，
即a的取值范围是：a＞1．
故答案为：a＞1．
点评 此题主要考查了不等式的解集问题，要熟练掌握，解答此题的关键是根据不等式的性质，判断出1-a＜0．
练习册系列答案
名校课堂系列答案
相关题目
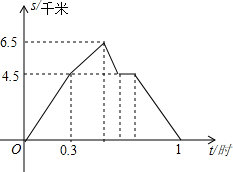从A到B地的一条公路，先是一段平路，然后是一段上坡路，小明骑自行车从A地出发，到达B地后立即按原路返回A地，返回途中休息了一段时间，假设小明骑车在平路、上坡路、下坡路时分别保持匀速前进．已知小明骑自行车在上坡路的速度比平路上的速度每小时少5千米．下坡路的速度比在平路上的速度每小时多5千米，小明在去B地和返回A地两次经过C地的时间间隔为0.15小时，小明离A地的路程S（单位：千米）和出发的时间t（单位：小时）之间的函数关系式如图所示．下列说法中正确的个数为（ ）
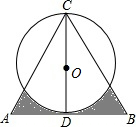如图，△ABC是边长为4的等边三角形，D为AB边的中点，以CD为直径画圆，则图中阴影部分的面积为2.5$\sqrt{3}$-π（结果保留π）．
16．某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料全部生产A、B两种产品共50件，生产A、B两种产品与所需原料情况如下表所示：
（1）该工厂生产A、B两种产品有哪几种方案？
（2）若生成一件A产品可获利80元，生产一件B产品可获利120元，怎样安排生产可获得最大利润？
| 原料 型号 | 甲种原料（千克） | 乙种原料（千克） |
| A产品（每件） | 9 | 3 |
| B产品（每件） | 4 | 10 |
（2）若生成一件A产品可获利80元，生产一件B产品可获利120元，怎样安排生产可获得最大利润？