题目内容
1.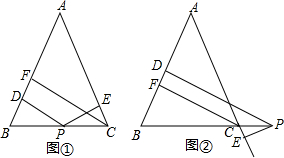 如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)
如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)
分析 可得CF+PE=PD,连接AP,根据等腰三角形的性质可表示出S△APB=S△ABC+S△ACP=$\frac{1}{2}$×AB×(CF+PE),同时可表示出S△APB=$\frac{1}{2}$AB×PD,从而可得到CF+PE=PD.
解答 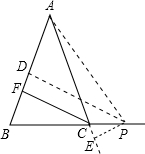 解:CF+PE=PD.
解:CF+PE=PD.
如图,连接AP,
∵AB=AC,
∴S△APB=S△ABC+S△ACP=$\frac{1}{2}$AB×CF+$\frac{1}{2}$AC×PE=$\frac{1}{2}$×AB×(CF+PE),
∵S△APB=$\frac{1}{2}$AB×PD,
∴CF+PE=PD.
点评 此题主要考查等腰三角形的性质及三角形面积的综合运用,此题的关键是利用面积公式将所求联系在一起.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列算式正确的是( )
| A. | -$\sqrt{(-3)^{2}}$=-3 | B. | (-$\sqrt{6}$)2=36 | C. | $\sqrt{16}$=±4 | D. | -(-$\sqrt{\frac{4}{9}}$)2=$\frac{4}{9}$ |
11.菱形周长为20,它的一条对角线长6,则菱形的另一条对角线长为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
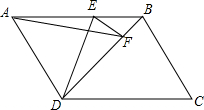 如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.
如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.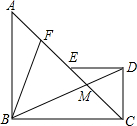 如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF.
如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF.