题目内容
13.关于x的方程kx2-6x+9=0有两个不相等的实数根.(1)求k的取值范围.
(2)若方程的一根为1,求k的值及方程的另一根.
分析 (1)为关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根,所以k≠0且△=b2-4ac>0,建立关于k的不等式组,解得k的取值范围即可;
(2)设方程的另一根为m,根据根与系数的关系,列方程组即可解得结果.
解答 解:(1)∵△=36-4k×9=36-36k>0,
∴k<1,
∵关于x的一元二次方程kx2-6x+9=0,k≠0,
∴k的取值范围为:k<1且k≠0;
(2)设方程的另一根为m,
∴$\left\{\begin{array}{l}{m+1=\frac{6}{k}}\\{m=\frac{9}{k}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-3}\\{k=-3}\end{array}\right.$,
∴k=-3,另一根为-3.
点评 本题考查了一元二次方程根的判别式的应用,根与系数的关系,方程的解,切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
15.下列因式分解错误的是( )
| A. | 2a-2b=2(a-b) | B. | x2-9=(x+3)(x-3) | C. | a2+4a-4=(a+2)2 | D. | -x2-x+2=-(x-1)(x+2) |
8.(1)$\sqrt{2}$+3$\sqrt{2}$-5$\sqrt{2}$
(2)|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|+$\sqrt{(-2)^{2}}$.
(2)|$\sqrt{3}$-$\sqrt{2}$|+|$\sqrt{3}$-2|+$\sqrt{(-2)^{2}}$.
18.若点P(3-a,a+2)在第四象限,则a的取值范围是( )
| A. | -2<a<3 | B. | a<3 | C. | a<-2 | D. | a>-2 |
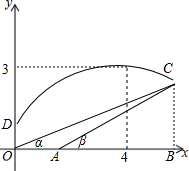 某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.
某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.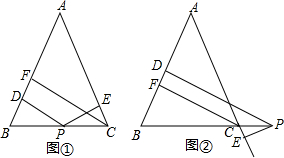 如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)
如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)