题目内容
15. 如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH.
如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH.
分析 由平行四边形的性质证出∠EBH=∠FDG,由ASA证△EBH≌△FDG,即可得出FG=EH.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∠A=∠C,
∴∠E=∠F,∠A=∠FDG,∠EBH=∠C,
∴∠EBH=∠FDG,
在△EBH与△FDG中,$\left\{\begin{array}{l}{∠E=∠F}&{\;}\\{BE=DF}&{\;}\\{∠EBH=∠FDG}&{\;}\end{array}\right.$,
∴△EBH≌△FDG(AAS),
∴FG=EH.
点评 本题考查了平行四边形的性质及全等三角形的判定;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.作为“一带一路”倡议的重大先行项目,中国、巴基斯坦经济走廊建设进展快、成效显著.两年来,已有18个项目在建或建成,总投资额达185亿美元.185亿用科学记数法表示为( )
| A. | 1.85×109 | B. | 1.85×1010 | C. | 1.85×1011 | D. | 1.85×1012 |
3. 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )
 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠1=∠2+∠3 | D. | ∠3=∠1+∠2 |
7.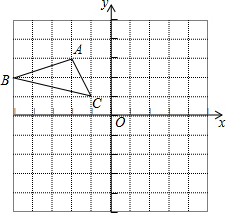 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
 如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )
如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是( )| A. | (-3,2) | B. | (2,-3) | C. | (1,-2) | D. | (-1,2) |
4.若分式$\frac{|x|-1}{x+1}$的值为零,则x的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |




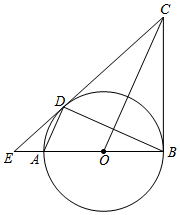 如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.