题目内容
20.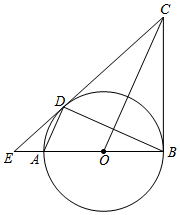 如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
分析 (1)首选连接OD,易证得△COD≌△COB(SAS),然后由全等三角形的对应角相等,求得∠CDO=90°,即可证得直线CD是⊙O的切线;
(2)设⊙O的半径为R,则OE=R+1,在Rt△ODE中,利用勾股定理列出方程,求解即可.
解答 解:(1)证明:连结DO.
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中
∵OD=OB,OC=OC,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO.
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,
又∵点D在⊙O上,
∴CD是⊙O的切线;
(2)设⊙O的半径为R,则OD=R,OE=R+1,
∵CD是⊙O的切线,
∴∠EDO=90°,
∴ED2+OD2=OE2,
∴32+R2=(R+1)2,
解得R=4,
∴⊙O的半径为4.
点评 本题主要考查的是切线的判断、圆周角定理的应用,掌握切线的判定定理,利用勾股定理列出关于r的方程是解题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
8.一元二次方程3x2-1=2x+5两实根的和与积分别是( )
| A. | $\frac{3}{2}$,-2 | B. | $\frac{2}{3}$,-2 | C. | $-\frac{2}{3}$,2 | D. | $-\frac{3}{2}$,2 |
5.如图是一个几何体的三视图,则这个几何体是( )


| A. | 三棱柱 | B. | 圆柱 | C. | 圆台 | D. | 圆锥 |
12. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
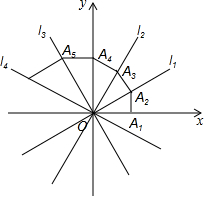 如图,四条直线l1:y1=$\frac{\sqrt{3}}{3}$x,l2:y2=$\sqrt{3}$x,l3:y3=-$\sqrt{3}$x,l4:y4=-$\frac{\sqrt{3}}{3}$x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为(($\frac{2\sqrt{3}}{3}$)2016,0).
如图,四条直线l1:y1=$\frac{\sqrt{3}}{3}$x,l2:y2=$\sqrt{3}$x,l3:y3=-$\sqrt{3}$x,l4:y4=-$\frac{\sqrt{3}}{3}$x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为(($\frac{2\sqrt{3}}{3}$)2016,0). 如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH.
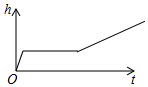
如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH.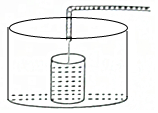 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )


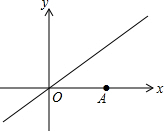 如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).
如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).