题目内容
3. 如右图,AB∥CD,则下列式子一定成立的是( )
如右图,AB∥CD,则下列式子一定成立的是( )| A. | ∠1=∠3 | B. | ∠2=∠3 | C. | ∠1=∠2+∠3 | D. | ∠3=∠1+∠2 |
分析 先根据平行线的性质,即可得到∠DFE=∠3,再根据三角形外角性质可得∠DEF=∠1+∠2,进而得到∠3=∠1+∠2.
解答  解:∵AB∥CD,
解:∵AB∥CD,
∴∠DFE=∠3,
∵∠DEF=∠1+∠2,
∴∠3=∠1+∠2.
故选D.
点评 本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.

练习册系列答案
相关题目
8.一元二次方程3x2-1=2x+5两实根的和与积分别是( )
| A. | $\frac{3}{2}$,-2 | B. | $\frac{2}{3}$,-2 | C. | $-\frac{2}{3}$,2 | D. | $-\frac{3}{2}$,2 |
12. 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
 如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,点A、B、C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
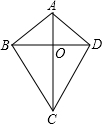 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中: 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-3,4),B(-5,2),C(-2,1).
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-3,4),B(-5,2),C(-2,1). 如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH.
如右图,在?ABCD中,E、F分别是AB、CD延长线上的点,且BE=DF,连接EF交AD、BC于点G、H.求证:FG=EH. 如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.