题目内容
10. 花盆摆放的图案如图所示:“○”表示红色郁金香,“□”表示黄色郁金香,请你仔细观察花盆摆放的规律,可得出前n行共有$\frac{1}{2}$n(n+1)盆红色郁金香和n(n+1)黄色郁金香.
花盆摆放的图案如图所示:“○”表示红色郁金香,“□”表示黄色郁金香,请你仔细观察花盆摆放的规律,可得出前n行共有$\frac{1}{2}$n(n+1)盆红色郁金香和n(n+1)黄色郁金香.
分析 通过分析可以发现,前n行中共有红色郁金香花盆数是:1+2+3+4+…+n;共有黄色郁金香花盆数是2+4+6+8+…+2n;由此进一步计算得出答案即可.
解答 解:由图形可知:
前n行有红色郁金香花共1+2+3+4+…+n=$\frac{1}{2}$n(n+1)盆;
黄色郁金香花共2+4+6+8+…+2n=n(n+1)盆.
故答案为:$\frac{1}{2}$n(n+1);n(n+1).
点评 此题考查图形的变化规律,关键是根据给出的图形,通过认真分析,归纳总结出数字运算的规律,利用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.将正方形图(1)作如下操作:第一次,分别连接对边中点,得图(2)有5个正方形;第二次,将图(2)右下角正方形按上述方法再分割成如图(3)有9个正方形,…以此类推,若要得到197个正方形,则需要操作的次数是( )


| A. | 48 | B. | 49 | C. | 50 | D. | 51 |
19.将方程3x2-x=-2(x+1)2化成一般形式后,一次项系数为( )
| A. | -5 | B. | 5 | C. | -3 | D. | 3 |
20.在数轴上,点A表示的数是-5,点C表示的数是4,若AB=2BC,则点B在数轴上表示的数是( )
| A. | 1或13 | B. | 1 | C. | 9 | D. | -2或10 |
 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值. 如图所示的正方形网格的边长为1,请你在图中作出一个边长为3的菱形.
如图所示的正方形网格的边长为1,请你在图中作出一个边长为3的菱形.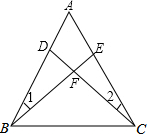 如图,在△ABC中,已知∠1=∠2,BE=CD.
如图,在△ABC中,已知∠1=∠2,BE=CD.