题目内容

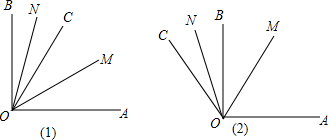
5．将正方形图（1）作如下操作：第一次，分别连接对边中点，得图（2）有5个正方形；第二次，将图（2）右下角正方形按上述方法再分割成如图（3）有9个正方形，…以此类推，若要得到197个正方形，则需要操作的次数是（　　）
A．48B．49C．50D．51

分析 由题意可知：第1次，分别连接各边中点如图2，得到4+1=5个正方形；第2次，将图2右上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形…，以此类推，根据以上操作，则第n次得到4n+1个正方形，由此建立方程求得答案即可．

解答 解：∵第1次，分别连接各边中点如图2，得到4+1=5个正方形；
第2次，将图2右上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形；
…
∴第n次得到4n+1个正方形；
则4n+1=197，
解得：n=49．
故选：B．

点评 此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键．

练习册系列答案
相关题目
5．已知$\frac{1}{a}$-$\frac{1}{b}$=2，则$\frac{ab}{2a+3ab-2b}$的值为（　　）
A．$\frac{1}{2}$B．-$\frac{1}{2}$C．1D．-1
16．一次函数，y=kx+b（k、b是常数，k≠0）的图象如图所示，则不等式kx+b＜0的解集是（　　）
A．x＞-2B．x＞0C．x＜-2D．x＜0
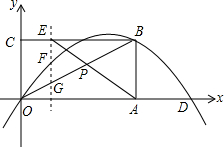13．如图，在平面直角坐标系xOy中，矩形OABC的边OA在x轴上，顶点B（4，2）在抛物线y=ax2+bx上，且抛物线交x轴于另一点D（6，0）．
（1）则a=-$\frac{1}{4}$，b=$\frac{3}{2}$；
（2）已知E为BC边上一个动点（不与B、C重合），连结AE交OB于点P，过点E作y轴的平行线分别交抛物线、直线OB于F、G．
①求线段FG的最大值，此时△PFG的面积为$\frac{1}{3}$；
②若以点O为圆心，OP为半径作⊙O，试判断直线AE与⊙O的能否相切？若能请求出E点坐标，若不能请说明理由．
20．如图，△ABC的三个顶点坐标分别为（0，2），（-3，0）和（4，0），动点P从原点O出发（点P不与点O重合），沿着x轴的正方向以每秒1个单位的速度匀速运动，过点P作直线l⊥x轴，设点P的运动时间为t（秒）
（1）操作：
①在图中画出△ABO以点O为旋转中心顺时针旋转90°的图形（记为△A′B′O′）．
②在图中画出△A′B′O′关于直线l对称的图形（记为△A″B″O″）．
（2）设△A″B″O″与△ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．
10．花盆摆放的图案如图所示：“○”表示红色郁金香，“□”表示黄色郁金香，请你仔细观察花盆摆放的规律，可得出前n行共有$\frac{1}{2}$n（n+1）盆红色郁金香和n（n+1）黄色郁金香．
17．已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC．
①若OC在∠AOB的内部，如图（1），求∠MON的度数；
②若OC在∠AOB的外部，如图（2），求∠MON的度数；
③若∠AOB=α，∠BOC=β，0°＜β＜α，α+β＜180°，其它条件不变，写出∠MON的度数．
14．（1）已知多项式-$\frac{2}{3}$x2ym+1+xy2-2x3+8是六次四项式，单项式-$\frac{3}{5}$x3ay5-m的次数与多项式的次数相同，求m，a的值；
（2）已知多项式mx4+（m-2）x3+（2n+1）x2-3x+n不含x2和x3的项，试写出这个多项式，再求当x=-1时多项式的值．
15．下列运算中，正确的是（　　）
A．a+2a=3a2B．4m-m=3C．2as+as=3asD．d2+d3=d5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网