题目内容
1. 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,求∠CDE的余弦值.
分析 先根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得AD=AE=5,∠DAE=∠BNAC=60°,CE=BD=6,于是可判断△ADE为等边三角形,得到DE=AD=5;过E点作EH⊥CD于H,如图,设DH=x,则CH=4-x,利用勾股定理得到52-x2=62-(4-x)2,解得x=$\frac{5}{8}$,然后根据余弦的定义求解.
解答 解:∵△ABC为等边三角形,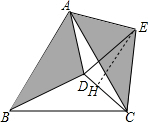
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转得△ACE,
∴AD=AE=5,∠DAE=∠BNAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5,
过E点作EH⊥CD于H,如图,设DH=x,则CH=4-x,
在Rt△DHE中,EH2=52-x2,
在Rt△CHE中,EH2=62-(4-x)2,
∴52-x2=62-(4-x)2,解得x=$\frac{5}{8}$,
∴DH=$\frac{5}{8}$,
在Rt△EDH中,cos∠HDE=$\frac{DH}{DE}$=$\frac{\frac{5}{8}}{5}$=$\frac{1}{8}$,
即∠CDE的余弦值为$\frac{1}{8}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和解直角三角形.

练习册系列答案
相关题目
1.凸四边形ABCD中,AB=3,BC=4,CD=7,则AD边的取值范围为( )
| A. | 2<AD<7 | B. | 2<AD<13 | C. | 0<AD<14 | D. | 1<AD<13 |
16. 一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
 一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )
一次函数,y=kx+b(k、b是常数,k≠0)的图象如图所示,则不等式kx+b<0的解集是( )| A. | x>-2 | B. | x>0 | C. | x<-2 | D. | x<0 |

 如图,一架25米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为7米.
如图,一架25米长的梯子AB,斜靠在一竖直的墙AC上,这时梯足B到墙底端C的距离为7米.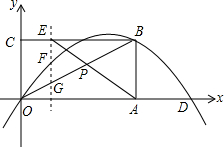 如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y=ax2+bx上,且抛物线交x轴于另一点D(6,0).
如图,在平面直角坐标系xOy中,矩形OABC的边OA在x轴上,顶点B(4,2)在抛物线y=ax2+bx上,且抛物线交x轴于另一点D(6,0). 花盆摆放的图案如图所示:“○”表示红色郁金香,“□”表示黄色郁金香,请你仔细观察花盆摆放的规律,可得出前n行共有$\frac{1}{2}$n(n+1)盆红色郁金香和n(n+1)黄色郁金香.
花盆摆放的图案如图所示:“○”表示红色郁金香,“□”表示黄色郁金香,请你仔细观察花盆摆放的规律,可得出前n行共有$\frac{1}{2}$n(n+1)盆红色郁金香和n(n+1)黄色郁金香. 如图,抛物线y=ax2+2x-6与x轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与x轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.