题目内容
11.已知一列数如下:$\frac{\sqrt{2}}{2},\frac{1}{2},\frac{\sqrt{6}}{6},\frac{\sqrt{2}}{4},\frac{\sqrt{10}}{10}$,…仔细观察这一列数,并回答问题:(1)第6个数是多少?
(2)第10个数是多少?
(3)你发现了什么规律?请你用n(正整数)来表示发现的规律.
分析 (1)利用已知得出第偶数个分子与分母的变化规律进而得出答案;
(2)利用已知得出第偶数个分子与分母的变化规律进而得出答案;
(3)利用已知得出第偶数与奇数个分子与分母的变化规律进而得出答案.
解答 解:(1)由题意可得:
第6个数是:$\frac{\sqrt{3}}{6}$;
(2)由题意可得:
第6个数是:$\frac{\sqrt{5}}{10}$;
(3)由已知可得:n为偶数时,第n个式子的分母为n,分子为$\sqrt{\frac{n}{2}}$,即$\frac{\sqrt{\frac{n}{2}}}{n}$;
n为奇数时,第n个式子的分母为2n,分子为$\sqrt{2n}$,即$\frac{\sqrt{2n}}{2n}$.
点评 此题主要考查了数字变化规律,根据题意得出分子与分母的变化规律是解题关键.

练习册系列答案
相关题目
6.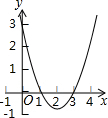 二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
 二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )
二次函数y=x2-4x+3的图象如图所示,利用图象可判断方程x2-4x+$\frac{10}{3}$=0较大的解所在的范围是( )| A. | 0<x<1 | B. | 1<x<2 | C. | 2<x<3 | D. | x>3 |
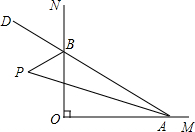 如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?
如图,已知∠MON=90°,点A、B分别是OM、ON上的动点,若P是∠BAO和∠ABO的外角∠OBD的角平分线的交点,则∠P的大小是否发生变化?为什么?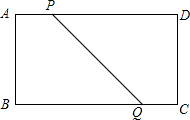 如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动
如图,四边形ABCD是矩形,AD=16cm,AB=8cm,动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,点Q以2cm/s的速度向B移动