题目内容
 如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长.
如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长.考点:平行四边形的判定与性质
专题:
分析:由条件可证明四边形AFDE为平行四边形,可得到AE=DF,再由AB=AC可证明BF=DF,可求得四边形AFDE的周长.
解答:解:∵DF∥AC,DE∥AB,
∴四边形AFDE为平行四边形,
∴DF=AE,
又∵AB=AC,
∴∠B=∠C,且DF∥AC,
∴∠FDB=∠C,
∴∠B=∠FDB,
∴BF=DF,
∴AE=BF,
∴AF+AE=AF+FB=AB,
∴AF+AE+DE+DF=2AB=10cm,
即四边形AFDE的周长为10cm.
∴四边形AFDE为平行四边形,
∴DF=AE,
又∵AB=AC,
∴∠B=∠C,且DF∥AC,
∴∠FDB=∠C,
∴∠B=∠FDB,
∴BF=DF,
∴AE=BF,
∴AF+AE=AF+FB=AB,
∴AF+AE+DE+DF=2AB=10cm,
即四边形AFDE的周长为10cm.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目
 如图,OA⊥OB,CO⊥DO,
如图,OA⊥OB,CO⊥DO,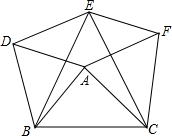 如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,
如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF,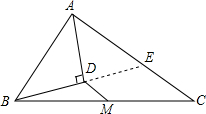 △ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D.
△ABC中,M为BC的中点,AD为∠BAC的平分线,BD⊥AD于D. 如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?
如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm的课本上的字0.3cm×0.2cm感觉相同(即视角相同)?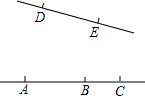 (1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有
(1)如图,以点A、B、C、D、E中的任意3点为顶点的三角形共有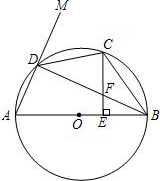 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是
 如图,A,B,C三点在⊙O上,∠A=40°,∠OCA=15°,OB,AC交于点D,则∠BDC的度数为
如图,A,B,C三点在⊙O上,∠A=40°,∠OCA=15°,OB,AC交于点D,则∠BDC的度数为 如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求:
如图,在平行四边形ABCD中,点M是BC的中点,AM⊥BD,AM交BD于点P.且AM=9,BD=12.试求: