题目内容
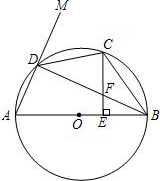 如图,AB是⊙O的直径,C是
如图,AB是⊙O的直径,C是 |
| BD |
(1)求证:CF=BF;
(2)若tan∠CDM=2,求sin∠ABD的值.
考点:圆周角定理,圆心角、弧、弦的关系,解直角三角形
专题:
分析:(1)首先延长CE交⊙O于点G,由AB是⊙O的直径,CE⊥AB,根据垂径定理可得:
=
,又由C是
的中点,即可证得
=
,由圆周角定理可得∠BCF=∠CBF,即可证得CF=BF;
(2)由圆的内接四边形的性质可得∠ABC=∠DCM,即可得tan∠ABC=
=2,然后设CE=2x,BE=x,可得BF=CF=CE-EF=2x-EF,又在Rt△BEF中,EF2+BE2=BF2,即可求得EF的长,继而求得答案.
 |
| BC |
 |
| BG |
 |
| BD |
 |
| CD |
 |
| BG |
(2)由圆的内接四边形的性质可得∠ABC=∠DCM,即可得tan∠ABC=
| CE |
| BE |
解答: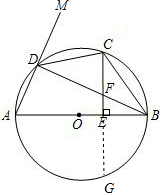 (1)证明:延长CE交⊙O于点G,
(1)证明:延长CE交⊙O于点G,
∵AB是⊙O的直径,CE⊥AB,
∴
=
,
∵C是
的中点,
∴
=
,
∴
=
,
∴∠BCF=∠CBF,
∴CF=BF;
(2)解:∵∠CDM+∠ADC=180°,∠ABC+∠ADC=180°,
∴∠ABC=∠DCM,
∵tan∠CDM=2,
∴tan∠ABC=
=2,
设CE=2x,BE=x,
∴BF=CF=CE-EF=2x-EF,
在Rt△BEF中,EF2+BE2=BF2,
∴EF2+x2=(2x-EF)2,
解得:EF=
x,
∴BF=2x-EF=
x,
∴sin∠ABD=
=
.
 (1)证明:延长CE交⊙O于点G,
(1)证明:延长CE交⊙O于点G,∵AB是⊙O的直径,CE⊥AB,
∴
 |
| BC |
 |
| BG |
∵C是
 |
| BD |
∴
 |
| CD |
 |
| BC |
∴
 |
| CD |
 |
| BG |
∴∠BCF=∠CBF,
∴CF=BF;
(2)解:∵∠CDM+∠ADC=180°,∠ABC+∠ADC=180°,
∴∠ABC=∠DCM,
∵tan∠CDM=2,
∴tan∠ABC=
| CE |
| BE |
设CE=2x,BE=x,
∴BF=CF=CE-EF=2x-EF,
在Rt△BEF中,EF2+BE2=BF2,
∴EF2+x2=(2x-EF)2,
解得:EF=
| 3 |
| 4 |
∴BF=2x-EF=
| 5 |
| 4 |
∴sin∠ABD=
| EF |
| BF |
| 3 |
| 5 |
点评:此题考查了圆周角定理、垂径定理、圆的内接四边形的性质、勾股定理以及锐角三角函数的知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,?OABC的顶点O在坐标原点,顶点A、C在反比例函数y=
如图,?OABC的顶点O在坐标原点,顶点A、C在反比例函数y= 如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点.
如图,AB为⊙O的直径,C为AE的中点,连结AE交BC于F点. 如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长.
如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,点E,F分别在AB,AC上,求四边形AFDE的周长. 已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=
已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=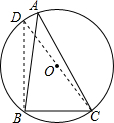 阅读材料,解答问题:
阅读材料,解答问题: 如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.
如图,以Rt△ABC的三边分别向外作三个正方形ACDE、BCNM、ABGH,其面积分别为S1,S2,S3,设Rt△ABC的两条直角边长为a,b,斜边长为c,请证明:S3=S1+S2.