题目内容
点P在y=
上，PA⊥x轴于A，PB⊥y轴于B，矩形PAOB绕y轴旋转一周所得的圆柱的侧面积为 ．
| 3 |
| x |
考点：反比例函数综合题
专题：
分析：设P的坐标是（x，y），则xy=3．PA=|y|，|PB|=|x|，则PA•PB=3，矩形PAOB绕y轴旋转一周所得的圆柱的底面半径是PB，高是PA，利用侧面积公式即可求解．
解答：解：设P的坐标是（x，y），则xy=3．PA=|y|，|PB|=|x|，则PA•PB=3．
矩形PAOB绕y轴旋转一周所得的圆柱的底面半径是PB，则底面周长是2π•PB，高是PA．
则圆柱的侧面积为：2π•PB•PA=2π×3=6π．
故答案是：6π．
矩形PAOB绕y轴旋转一周所得的圆柱的底面半径是PB，则底面周长是2π•PB，高是PA．
则圆柱的侧面积为：2π•PB•PA=2π×3=6π．
故答案是：6π．
点评：本题考查了圆柱的侧面积的计算，正确根据函数的解析式得到PA•PB=3是解题的关键．
练习册系列答案
相关题目
若abc=1，且
+
+
=2003．则x等于（ ）
| x |
| 1+a+ab |
| x |
| 1+b+bc |
| x |
| 1+c+ac |
| A、1 | B、2003 |
| C、4006 | D、2008 |
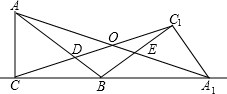（S△AOD+S△A1BE）-（S△C1OE+S△CBD）=