题目内容
利用乘法公式计算：
（1）（x+2y）（x-2y）-（x-4y）2-4y（2x-y）
（2）（a-2b-3）（a+2b-3）-（a-2b+3）2．
（1）（x+2y）（x-2y）-（x-4y）2-4y（2x-y）
（2）（a-2b-3）（a+2b-3）-（a-2b+3）2．
考点：完全平方公式,平方差公式
专题：
分析：（1）根据平方差公式和完全平方公式进行计算即可；
（2）根据平方差公式和完全平方公式进行计算即可．
（2）根据平方差公式和完全平方公式进行计算即可．
解答：解：（1）原式=x2-4y2-x2+8xy-16y2-8xy+4y2
=-16y2；
（2）原式=[（a-3）-2b][（a-3）+2b]-（a-2b+3）2
=（a-3）2-4b2-（a+3）2+4b（a+3）-4b2
=-12a-8b2+4ab+12b．
=-16y2；
（2）原式=[（a-3）-2b][（a-3）+2b]-（a-2b+3）2
=（a-3）2-4b2-（a+3）2+4b（a+3）-4b2
=-12a-8b2+4ab+12b．
点评：本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
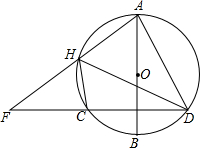已知AB是⊙O的直径，弦CD⊥AB于点E，H是
如图所示，已知E为菱形ABCD的边AD的中点，EF⊥AC于F交AB于M，试说明M为AB的中点．
如图，将一副三角板的直角顶点重合，若∠AOD=50°，则∠COB=
如图，已知∠AOB=30°，∠BOC=71°，OE平分∠AOC，求∠BOE的度数．（精确到分）
如图，Rt△ABC中，AB=BC=8，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，下列结论：①△BDN的周长为12；②M是AC的中点； ③∠CMD+∠BND=90°；④DM=DN，其中正确的是数轴上与原点距离4个单位长度的点所表示的有理数是（ ）
| A、4 | B、-4 | C、±4 | D、无法确定 |