题目内容
某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元其销售量就减少20件.
(1)当售价定为12元时,每天可售出 件;
(2)要使每天利润达到640元,则每件售价应定为多少元?
(3)当每件售价定为多少元时,每天获得最大利润?并求出最大利润.
(1)当售价定为12元时,每天可售出
(2)要使每天利润达到640元,则每件售价应定为多少元?
(3)当每件售价定为多少元时,每天获得最大利润?并求出最大利润.
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)由原来的销量-减少的销量就可以得出现在的销量而得出结论;
(2)由利润=每件利润×销售数量建立方程求出其解即可;
(3)设每天获得的利润为W元,由利润=每件利润×销售数量建立W与x的关系式,由二次函数的性质就可以求出结论.
(2)由利润=每件利润×销售数量建立方程求出其解即可;
(3)设每天获得的利润为W元,由利润=每件利润×销售数量建立W与x的关系式,由二次函数的性质就可以求出结论.
解答:解:(1)由题意,得
200-20×(12-10)=160.
故答案为:160;
(2)设每件售价定为x元,由题意,得
(x-8)[200-20(x-10)]=640,
解得x1=16,x2=12.
答:要使每天利润达到640元,则每件售价应定为16或12元;
(3)设售价为x元,每天的利润为W元,由题意,得
W=(x-8)[200-20(x-10)]
W=-20x2+560x-3200,
W=-20(x-14)2+720.
∵a=-20<0,
∴x=14时,W最大=720.
答:当每件售价定为14元时,每天获得最大利润,为720元.
200-20×(12-10)=160.
故答案为:160;
(2)设每件售价定为x元,由题意,得
(x-8)[200-20(x-10)]=640,
解得x1=16,x2=12.
答:要使每天利润达到640元,则每件售价应定为16或12元;
(3)设售价为x元,每天的利润为W元,由题意,得
W=(x-8)[200-20(x-10)]
W=-20x2+560x-3200,
W=-20(x-14)2+720.
∵a=-20<0,
∴x=14时,W最大=720.
答:当每件售价定为14元时,每天获得最大利润,为720元.
点评:本题考查了销售问题的数量关系利润=每件利润×销售数量的运用,二次函数的解析式的运用,二次函数的顶点式的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等边三角形 | B、平行四边形 |
| C、菱形 | D、梯形 |
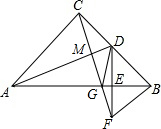 如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.
如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG. 如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O是矩形ABCD对角线的交点,DE∥AC,CE∥BD. 如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M,试说明M为AB的中点.
如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M,试说明M为AB的中点. 如图,已知∠AOB=30°,∠BOC=71°,OE平分∠AOC,求∠BOE的度数.(精确到分)
如图,已知∠AOB=30°,∠BOC=71°,OE平分∠AOC,求∠BOE的度数.(精确到分)