题目内容
6.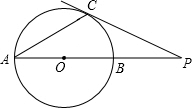 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )| A. | 5$\sqrt{3}$ | B. | 5 | C. | 10 | D. | $\frac{5\sqrt{3}}{3}$ |
分析 连接OC,如图,利用切线的性质得到OC⊥PC,再利用等腰三角形的性质和三角形外角性质计算出∠POC=60°,然后在Rt△OCA中利用含30度的直角三角形三边的关系求解.
解答 解: 连接OC,如图,
连接OC,如图,
∵PC为切线,
∴OC⊥PC,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
在Rt△OCA中,PC=$\sqrt{3}$OC=5$\sqrt{3}$.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
14.正方形的正投影不可能是( )
| A. | 正方形 | B. | 长方形 | C. | 线段 | D. | 梯形 |
1.关于x的方程kx2+4x+4=0有实数根,则k的取值范围是( )
| A. | k<1 | B. | k<1且k≠0 | C. | k≤1 | D. | k≤1且k≠0 |
18.下列计算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2+a4=a6 | C. | (-$\frac{1}{3}$)-1=$\frac{1}{3}$ | D. | (-π)0=1 |
15.已知某圆锥的底面直径为6cm,母线长4cm,则它的全面积为( )
| A. | 21πcm2 | B. | 60π cm2 | C. | 24π cm2 | D. | 12π cm2 |
16.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=$\frac{9}{2}$;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

 某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)