题目内容
17.如图,正方形ABCD的边长是5,圆D的半径是3,在圆D上任取一点P,连接AP,将AP顺时针旋转90°到AP′,连接BP′.发现:不论点P在圆D上的什么位置,BP′的大小不变,BP′的长是3.
思考:(1)△APD的最大面积是7.5;点P与P′之间的最小距离是2$\sqrt{2}$;当点P与点B之间的距离最大时,∠CBP′的度数是45°.
探究:当AP与圆D相切时,求△CDP′的面积.
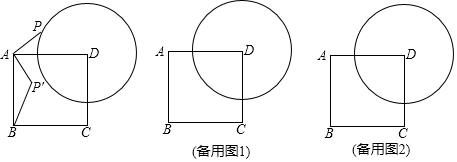
分析 发现:连接DP,由旋转的性质得:AP'=AP,∠PAP'=90°,由正方形的性质得出BC=AB=AD=5,∠BAD=90°,证出∠BAP'=∠DAP,由SAS证明△ABP'≌△ADP,得出BP'=DP=3即可;
思考:当PD⊥AD时,△APD的面积最大=$\frac{1}{2}$×5×3=7.5;当P在AD上时,PP'最小,此时P'在AB上,AP'=AP=2,由勾股定理得出PP'=2$\sqrt{2}$;当点P在射线BD上时,点P与点B之间的距离最大,此时∠ABP'=∠ADP=135°,求出∠CBP'°=45°即可;
探究:分两种情况:①如图所示:连接DP、DP'、CP',过点P'作AB的垂线,交AB于F,交CD于E,则EF⊥CD,EF=BC=5,由切线的性质得出∠APD=90°,由发现得:△ABP'≌△ADP,得出∠AP'B=∠APD=90°,由勾股定理得出AP'=AP=$\sqrt{A{D}^{2}-D{P}^{2}}$=4,在Rt△ABP'中,由三角形面积求出P'F=$\frac{12}{5}$,得出P'E=$\frac{13}{5}$,即可求出△CDP'的面积;
②如图所示:DP、DP'、CP',过点P'作AB的垂线,交AB于F,交CD于E,同理得:P'F=$\frac{3×4}{5}$=$\frac{12}{5}$,得出P'E=5+$\frac{12}{5}$=$\frac{37}{5}$,即可求出△CDP'的面积.
解答  发现:
发现:
解:连接DP,如图1所示:
由旋转的性质得:AP'=AP,∠PAP'=90°,
∵四边形ABCD是正方形,
∴BC=AB=AD=5,∠BAD=90°,
∴∠BAD-∠DAP'=∠PAP'-∠DAP',
即∠BAP'=∠DAP,
在△ABP'和△ADP中,$\left\{\begin{array}{l}{AP'=AP}&{\;}\\{∠BAP'=∠DAP}&{\;}\\{AB=AD}&{\;}\end{array}\right.$,
∴△ABP'≌△ADP(SAS),
∴BP'=DP=3;
故答案为:3;
思考:
解:当PD⊥AD时,如图2所示:
△APD的面积最大=$\frac{1}{2}$×5×3=7.5;
当P在AD上时,PP'最小,
此时P'在AB上,AP'=AP=5-3=2,
∵∠PAP'=90°,
∴PP'=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
当点P在射线BD上时,如图3所示:
点P与点B之间的距离最大,
此时∠ABP'=∠ADP=180°-45°=135°,
∴∠CBP'=135°-90°=45°;
故答案为:7.5;2$\sqrt{2}$;45°;
探究:
解:分两种情况:①如图4所示:
连接DP、DP'、CP',过点P'作AB的垂线,交AB于F,交CD于E,
则EF⊥CD,EF=BC=5,
∵AP是圆D的切线,
∴∠APD=90°,
由发现得:△ABP'≌△ADP,
∴∠AP'B=∠APD=90°,AP'=AP=$\sqrt{A{D}^{2}-D{P}^{2}}$=4,
在Rt△ABP'中,P'F=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴P'E=5-$\frac{12}{5}$=$\frac{13}{5}$,
∴△CDP'的面积=$\frac{1}{2}$×5×$\frac{13}{5}$=$\frac{13}{2}$;
②如图5所示:DP、DP'、CP',过点P'作AB的垂线,交AB于F,交CD于E,
同理得:P'F=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴P'E=5+$\frac{12}{5}$=$\frac{37}{5}$,
∴△CDP'的面积=$\frac{1}{2}$×5×$\frac{37}{5}$=$\frac{37}{2}$;
综上所述,当AP与圆D相切时,△CDP′的面积为$\frac{13}{2}$或$\frac{37}{2}$.
点评 本题是圆的综合题目,考查了旋转的性质、全等三角形的判定与性质、正方形的性质、勾股定理、切线的性质、三角形面积的计算、分类讨论等知识;本题综合性强,有一定难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{9}{37}$ | B. | $\frac{11}{37}$ | C. | $\frac{10}{31}$ | D. | $\frac{7}{39}$ |
| A. | x2+x2=x4 | B. | x2•x3=x6 | C. | (-2x3)2=-4x6 | D. | (x3)2=x6 |
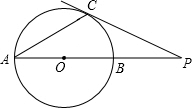 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线于P.若圆半径等于5,则线段CP的长度是( )| A. | 5$\sqrt{3}$ | B. | 5 | C. | 10 | D. | $\frac{5\sqrt{3}}{3}$ |
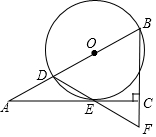 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
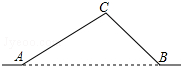 如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
 某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题: