题目内容
20．已知x为实数，且ax4+bx3+cx2+dx+e=（2x-1）4，则a+c的值为40．分析 首先将（2x-1）4展开，并分别求出a、c的值各是多少，然后把a、c的值相加，求出它们的和是多少即可．
解答 解：∵ax4+bx3+cx2+dx+e=（2x-1）4=16x4-32x3+24x2-8x+1，
∴a=16，b=-32，c=24，d=-8，e=1，
∴a+c=16+24=40，
即a+c的值为40．
故答案为：40．
点评 此题主要考查了代数式求值问题，要熟练掌握，解答此题的关键是将（2x-1）4展开，并分别求出a、c的值各是多少．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图是由9个等边三角形拼成的六边形，若已知中间的小等边三角形的边长是2，则六边形的周长是60．
在△ABC中，D，E分别为AB，AC上一点，DE交AF于H，HG⊥BC，连接DG，GE．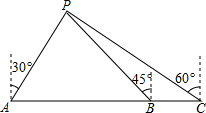
天宜号船向正东方航行（如图），船在A处时测得灯塔在P北偏东30°方向，前进到B处时测得灯塔P恰好在西北方向，又航行半小时到达C处，此时测得灯塔P在北偏西60°方向，若船速为每小时20海里，求A、C两点间的距离．