题目内容
7.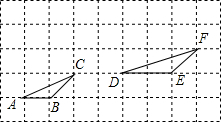 如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论.
如图,小正方形的边长均为1.图中的两个三角形是否相似?证明你的结论.
分析 由勾股定理求出BC、EF、AC、DF的长,得出三边成比例,即可得出结论.
解答 解:△ABC∽△FED;理由如下:
由勾股定理得:BC=EF=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,DF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵AB=1,DE=2,
∴$\frac{AB}{EF}=\frac{BC}{DE}=\frac{AC}{DF}$=$\frac{\sqrt{2}}{2}$,
∴△ABC∽△FED.
点评 本题考查了相似三角形的判定方法、正方形的性质、勾股定理;熟练掌握勾股定理,熟记三边成比例的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
17.多项式-x2-$\frac{1}{2}$x-1的各项分别是( )
| A. | -x2,$\frac{1}{2}$x,1 | B. | -x2,-$\frac{1}{2}$x,-1 | C. | x2,$\frac{1}{2}$x,1 | D. | 以上答案都不对 |
12.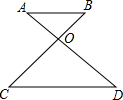 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
 如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )
如图,AB∥CD,AD与BC交于点O,已知AB=2,CD=3,则△AOB与△COD的面积比是( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{4}{3}$ |
16.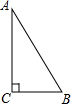 如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
 如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
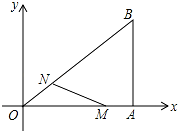 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题: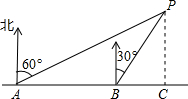 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?($\sqrt{3}$取1.732,结果精确到1米)
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?($\sqrt{3}$取1.732,结果精确到1米)