题目内容
2.一张纸,第一次把它分成5张,第二次把其中的一张分成5张,以后每一次都把前面所得的其中的一张分割成5张,如此进行下去…把下面的表格填写完整:| 操作次数 | 第一次 | 第2次 | 第3次 | 第4次 | 第5次 | … | 第n次 |
| 纸片张数 | 5 | 9 | 13 | 17 | 21 | 4n+1 |
分析 由题意可知:第一次分成5张,第二次分成5+4=9张,第三次分成5+4+4=13张,…每一次都比前面的多出4张,由此得出第n次分成的张数为5+4(n-1)=4n+1.
解答 解:填表如下:
| 操作次数 | 第一次 | 第2次 | 第3次 | 第4次 | 第5次 | … | 第n次 |
| 纸片张数 | 5 | 9 | 13 | 17 | 21 | 4n+1 |
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字的运算规律解决问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
12.代数式-3x2y,0,6x+y,$\frac{x+y}{4}$,$\frac{b}{a}$中,单项式的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知点A、B在直线l的同侧,在l上求作一点M,使得AM+BM最小.
如图,已知点A、B在直线l的同侧,在l上求作一点M,使得AM+BM最小. 一辆轿车在高速公路上匀速行驶.它在经过如下图所示的标志牌下时.速度已达40m/s,并仍以此速度在向前开行.
一辆轿车在高速公路上匀速行驶.它在经过如下图所示的标志牌下时.速度已达40m/s,并仍以此速度在向前开行.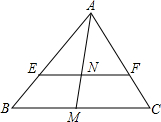 在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.
在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.