题目内容
12.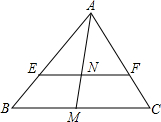 在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.
在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.
分析 由已知条件:△AEF的面积:△ABC的面积=2:5,通过△AEF∽△ABC,得到$\frac{AE}{AB}=\sqrt{\frac{{S}_{AEF}}{{S}_{△ABC}}}$=$\frac{\sqrt{10}}{5}$,由于△AEN∽△ABM,得到$\frac{AN}{AM}=\frac{AE}{AB}$=$\frac{\sqrt{10}}{5}$,即可得到结论.
解答 解:∵△AEF的面积:梯形BCFE的面积=2:3,
∴△AEF的面积:△ABC的面积=2:5,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AE}{AB}=\sqrt{\frac{{S}_{AEF}}{{S}_{△ABC}}}$=$\frac{\sqrt{10}}{5}$,
∵EF∥BC,
∴△AEN∽△ABM,
∴$\frac{AN}{AM}=\frac{AE}{AB}$=$\frac{\sqrt{10}}{5}$,
∵AM=15,
∴AN=3$\sqrt{10}$.
故答案为:3$\sqrt{10}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.一张纸,第一次把它分成5张,第二次把其中的一张分成5张,以后每一次都把前面所得的其中的一张分割成5张,如此进行下去…把下面的表格填写完整:
| 操作次数 | 第一次 | 第2次 | 第3次 | 第4次 | 第5次 | … | 第n次 |
| 纸片张数 | 5 | 9 | 13 | 17 | 21 | 4n+1 |
 如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.
如图,∠A0B内有-点P,在0A、0B上分别找点M、N,使△PMN的周长最小.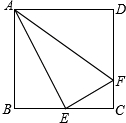 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.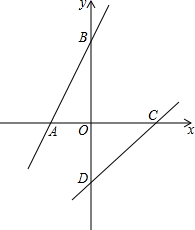 直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.
直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.