题目内容
16.下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( )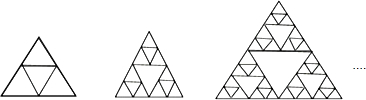
| A. | 160 | B. | 161 | C. | 162 | D. | 163 |
分析 由图可以看出:第一个图形中由角上的3个三角形加上中间1个小三角形再加上外围1个大三角形共有5个正三角形;下一个图形的三个角上的部分是上一个图形的全部,另外加上中间一个小的三角形和外围的一个大三角形,所以第二个图形中有5×3+1+1=17个正三角形,第三个图形中有17×3+1+1=53个正三角形,第四个图形中有53×3+1+1=161个正三角形.
解答 方法一:
解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:
$\stackrel{4×3}{\overbrace{5,17}}$,$\stackrel{4×{3}^{2}}{\overbrace{17,53}}$,$\stackrel{4×{3}^{3}}{\overbrace{53,161}}$,$\stackrel{4×{3}^{4}}{\overbrace{161,{a}_{5}}}$,…$\stackrel{4×{3}^{n-1}}{\overbrace{{a}_{n-1},{a}_{n}}}$,
∴$\left\{\begin{array}{l}{{a}_{2}-{a}_{1}=4×3}\\{{a}_{3}-{a}_{2}=4×{3}^{2}}\\{…}\\{{a}_{n}-{a}_{n-1}=4×3+4×{3}^{n-1}}\end{array}\right.$,
⇒(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)=an-a1,
∴an-a1=4×(3+32+…+3n-1)=4×(3+32+…+3n-1)=$\frac{{3}^{n}-3}{2}$(用错位相减法可求出)
∴${a}_{n}-{a}_{1}=2×{3}^{n}-6$,
∵a1=5,
∴${a}_{n}=2×{3}^{n}-1$.
点评 此题考查图形的变化规律,找出数字与图形之间的联系,找出规律解决问题是解答此题的关键.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )
如图,已知⊙O的直径AB⊥CD于点E,则下列结论一定错误的是( )| A. | CE=DE | B. | AE=OE | C. | $\widehat{BC}$=$\widehat{BD}$ | D. | △OCE≌△ODE |
 右边几何体的俯视图是( )
右边几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | $\sqrt{\frac{1}{16}}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | $\root{3}{9}$ |
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ |
| A. | 1000 | B. | 1000名 | ||
| C. | 1000名学生 | D. | 1000名考生的数学试卷 |
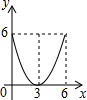
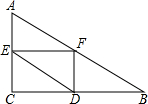 已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )
已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,点E是边AC上一动点,过点E作EF∥BC,交AB边于点F,点D为BC上任一点,连接DE,DF.设EC的长为x,则△DEF的面积y关于x的函数关系大致为( )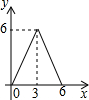
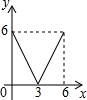
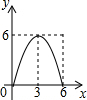
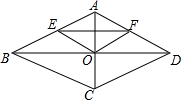 如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.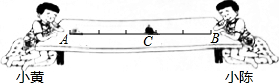 如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,那么还需要多长时间才能到达B点?
如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,那么还需要多长时间才能到达B点?