题目内容
已知|x-1|+(2y+1)2+(4z+2)2=0,则2x-y+z= .
考点:解三元一次方程组,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据题意,结合非负数的性质,得到x-1=0,2y+1=0,4z+2=0;解得x、y、z的值,代入所给的代数式计算,即可解决问题.
解答:解:∵|x-1|+(2y+1)2+(4z+2)2=0,
且|x-1|≥0,(2y+1)2≥0,(4z+2)2≥0,
∴x-1=0,2y+1=0,4z+2=0;
∴x=1,y=-
,z=-
,
∴2x-y+z=2+
-
=2.
故答案为2.
且|x-1|≥0,(2y+1)2≥0,(4z+2)2≥0,
∴x-1=0,2y+1=0,4z+2=0;
∴x=1,y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴2x-y+z=2+
| 1 |
| 2 |
| 1 |
| 2 |
故答案为2.
点评:该题主要考查了非负数的性质、三元一次方程组的解法等代数知识点的应用问题;解题的关键是深入观察、准确判断、正确解答.

练习册系列答案
相关题目
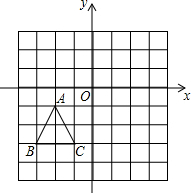 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3).
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3). 某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示:
某菜农搭建的一个横截面为抛物线的蔬菜大棚,尺寸如图所示: 如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE=
如图,等边△ABC中,延长AB至D,使BD=AB,延长AC至E,使CE=