题目内容
观察下列算式:
1×2×3×4+1=52=25
2×3×4×5+1=112=121
3×4×5×6+1=192=361
(1)请仿照上述算式规律计算4×5×6×7+1的值.(须体现过程)
(2)设n为上述算式中四个连续正整数之积中最小的整数,试用含n的等式表示上述规律.
1×2×3×4+1=52=25
2×3×4×5+1=112=121
3×4×5×6+1=192=361
(1)请仿照上述算式规律计算4×5×6×7+1的值.(须体现过程)
(2)设n为上述算式中四个连续正整数之积中最小的整数,试用含n的等式表示上述规律.
考点:规律型:数字的变化类
专题:
分析:(1)根据给出的式子发现:任意四个连续正整数的积与1的和一定是一个完全平方数,是两端的整数乘积加1的平方;
(2)由以上规律得出:即四个连续的正整数为n、(n+1)、(n+2)、(n+3),则n(n+1)(n+2)(n+3)+1=(n2+3n+1)2,据此解答.
(2)由以上规律得出:即四个连续的正整数为n、(n+1)、(n+2)、(n+3),则n(n+1)(n+2)(n+3)+1=(n2+3n+1)2,据此解答.
解答:解:(1)4×5×6×7+1
=(4×7+1)2
=292
=841;
(2)四个连续的正整数为n、(n+1)、(n+2)、(n+3),则n(n+1)(n+2)(n+3)+1=(n2+3n+1)2.
=(4×7+1)2
=292
=841;
(2)四个连续的正整数为n、(n+1)、(n+2)、(n+3),则n(n+1)(n+2)(n+3)+1=(n2+3n+1)2.
点评:此题考查数字的变化规律,关键是根据给出的式子,找出式子变化的规律,再由规律解决问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 一个实物的三视图如图,则这个实物形状可能是( )
一个实物的三视图如图,则这个实物形状可能是( )| A、圆柱 | B、三棱柱 |
| C、四棱柱 | D、五棱柱 |
 如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )
如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列变形错误的是( )
| A、若a=b,则5a=5b | ||||
| B、若a=b,则3-a=3-b | ||||
| C、若am=bm,则a=b | ||||
D、若
|
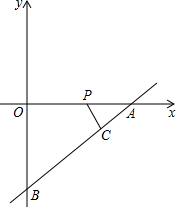 如图,直线y=
如图,直线y= 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.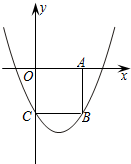 如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=
如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=