题目内容
5.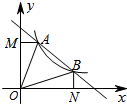 如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )
如图,已知直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交 于A、B两点,连接OA、OB,AM⊥y轴于点M,BN⊥x轴于点N,下列结论:①OA=OB;②△AOM≌△BON;③当AB=$\sqrt{2}$时,ON=BN=1.④若∠AOB=45°,则S△AOB=k;其中结论正确的是( )| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
分析 ①②设A(x1,y1),B(x2,y2),联立y=-x+b与y=$\frac{k}{x}$,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;
③延长MA,NB交于G点,可证△ABG为等腰直角三角形,当AB=时,GA=GB=1,则ON-BN=GN-BN=GB=1;
④作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k.
解答 解:设A(x1,y1),B(x2,y2),代入y=$\frac{k}{x}$,中,得x1•y1=x2•y2=k,
联立$\left\{\begin{array}{l}{y=-x+b}\\{y=\frac{k}{x}}\end{array}\right.$,得x2-bx+k=0,
则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴②△AOM≌△BON,故本选项正确;
①由②可知,OA=OB,故本选项正确;
③如图1,延长MA,NB交于G点,
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=$\sqrt{2}$时,GA=GB=1,
∴ON-BN=GN-BN=GB=1,
∴当AB=$\sqrt{2}$时,ON-BN=1,故本选项正确;
④如图2,作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵①△AOM≌△BON,故本选项正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=$\frac{1}{2}$k+$\frac{1}{2}$k=k,故本选项正确.
故选D.
点评 本题主要考查反比例函数与一次函数的交点,能利用待定系数法求出点的坐标,综合运用全等三角形和等腰直角三角形的性质是解决此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | y=2x-14 | B. | y=-x-6 | C. | y=-x+10 | D. | y=4x |
| A. | $\sqrt{3}$ | B. | $\sqrt{3}$-2 | C. | 2 | D. | -2 |
| A. | -34 | B. | -9 | C. | 0 | D. | 28 |
 如图,在四边形ABCD中,∠B=60°,∠BCD=90°,AB=BC=8,E为BC的中点,连结DE,若DE平分∠ADC,则△ECD的面积是8$\sqrt{3}$-8$\sqrt{2}$.
如图,在四边形ABCD中,∠B=60°,∠BCD=90°,AB=BC=8,E为BC的中点,连结DE,若DE平分∠ADC,则△ECD的面积是8$\sqrt{3}$-8$\sqrt{2}$.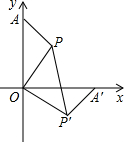 如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).
如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).