题目内容
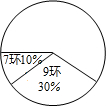 在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:
在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 3 | 2 |
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
考点:方差,统计表,扇形统计图
专题:
分析:(1)根据统计表(图)中提供的信息,可列式得命中环数是7环的次数是10×10%,10环的次数是10-3-2-1,再分别求出命中环数是8环和10环的圆心角度数画图即可,
(2)先求出甲运动员10次射击的平均成绩和方差,再与乙比较即可.
(2)先求出甲运动员10次射击的平均成绩和方差,再与乙比较即可.
解答:解:(1)命中环数是7环的次数是10×10%=1(次),10环的次数是10-3-2-1=4(次),
命中环数是8环的圆心角度数是;360°×
=72°,10环的圆心角度数是;360°×
=144°,
画图如下:

故答案为:4,1;
(2)∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,
∴甲运动员10次射击的方差=
[(10-9)2×4+(9-9)2×3+(8-9)2×2+(7-9)2]=1,
∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,
∴如果只能选一人参加比赛,认为应该派甲去.
命中环数是8环的圆心角度数是;360°×
| 2 |
| 10 |
| 4 |
| 10 |
画图如下:

故答案为:4,1;
(2)∵甲运动员10次射击的平均成绩为(10×4+9×3+8×2+7×1)÷10=9环,
∴甲运动员10次射击的方差=
| 1 |
| 10 |
∵乙运动员10次射击的平均成绩为9环,方差为1.2,大于甲的方差,
∴如果只能选一人参加比赛,认为应该派甲去.
点评:本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点P在x轴的下侧,y轴的左侧,距离每个坐标轴都是3个单位长度,则点P的坐标为( )
| A、(3,3) |
| B、(-3,3) |
| C、(-3,-3) |
| D、(3,-3) |
 如图为不完整的正方体平面展开图,需补上一块,请画出两种情况.
如图为不完整的正方体平面展开图,需补上一块,请画出两种情况. 实数a、b在数轴上的位置如图所示,化简
实数a、b在数轴上的位置如图所示,化简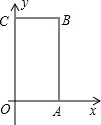 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且 如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作: 如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么.
如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么. 已知,如图,CD的平分∠ACB,DE∥BC,交AC于E,若∠AED=60°,求∠EDC的度数.
已知,如图,CD的平分∠ACB,DE∥BC,交AC于E,若∠AED=60°,求∠EDC的度数.