题目内容
18．
如图，∠ACB=90°，AC=BC，AD⊥CE于D，BE⊥CD于E，AD=2.4cm，DE=1.7cm，则BE的长度为0.7cm．
分析 先证明△BCE≌△CAD，得AD=CE=2.4，BE=CD，求出CD即可解决问题．
解答 解：∵AD⊥CE于D，BE⊥CD于E，
∴∠E=∠ADC=90°
∵AC=CB，∠ACB=90，
∴∠BCE+∠ACD=90°，∠ACD+∠DAC=90°，
∴∠BCE=∠ACD，
∴△BCE≌△CAD，
∴AD=CE=2.4，BE=CD，
∴CD=CE-DE=2.4-1.7=0.7，
∴BE=CD=0.7cm．
故答案为0.7cm．
点评 本题考查全等三角形的判定和性质、等角的余角相等等知识，解题的关键是熟练掌握全等三角形的判定，属于中考常考题型．
练习册系列答案
相关题目
8．
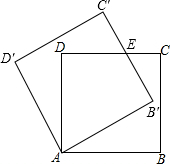如图，边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′，边B′C′与CD交于点E，则四边形AB′ED的面积是（ ）
如图，边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′，边B′C′与CD交于点E，则四边形AB′ED的面积是（ ）| A． | $\frac{3}{4}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |
13．为了节约资源，科学指导居民改善居住条件，小强向房管部门提出了一个购买商品房的政策性方案：
设一个3口之家购买商品房的人均面积为x平方米，缴纳房款y万元．
（1）请求出y关于x的函数关系式；
（2）若某3人之家欲购买120平方米的商品房，求其应缴纳的房款．
| 人均住房面积（平方米） | 单价（万元/平方米） |
| 不超过30（平方米）部分 | 0.4 |
| 超过30平方米部分 | 0.9 |
（1）请求出y关于x的函数关系式；
（2）若某3人之家欲购买120平方米的商品房，求其应缴纳的房款．
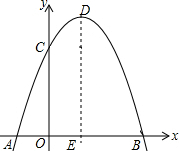如图，过点A（-1，0）、B（3，0）的抛物线y=-x2+bx+c与y轴交于点C，它的对称轴与x轴交于点E．