题目内容
8.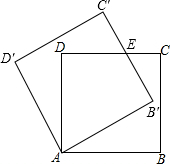 如图,边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′,边B′C′与CD交于点E,则四边形AB′ED的面积是( )
如图,边长为1的正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′,边B′C′与CD交于点E,则四边形AB′ED的面积是( )| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
分析 连结AE,如图,根据正方形和旋转的性质得∠BAB′=30°,AB=AB′AD,∠B=∠B′=90°,则∠DAB′=60°,再利用“HL”证明Rt△ADE≌Rt△AB′E得到∠DAE=∠B′AE=30°,接着根据含30度的直角三角形三边的关系计算出DE=$\frac{\sqrt{3}}{3}$AD=$\frac{\sqrt{3}}{3}$,然后根据三角形面积公式,利用四边形AB′ED的面积=2S△ADE求解即可.
解答 解:连结AE,如图,
∵正方形ABCD绕点A逆时针旋转30°得正方形AB′C′D′,
∴∠BAB′=30°,AB=AB′AD,∠B=∠B′=90°,
∴∠DAB′=60°,
在Rt△ADE和Rt△AB′E中,
$\left\{\begin{array}{l}{AE=AE}\\{AD=AB′}\end{array}\right.$,
∴Rt△ADE≌Rt△AB′E,
∴∠DAE=∠B′AE=30°,
在Rt△ADE中,∵∠DAE=30°,
∴DE=$\frac{\sqrt{3}}{3}$AD=$\frac{\sqrt{3}}{3}$,
∴S△ADE=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$,
∴四边形AB′ED的面积=2S△ADE=$\frac{\sqrt{3}}{3}$.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是连结AE,证明Rt△ADE≌Rt△AB′E.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
20.对(x2)3运算结果描述正确的是( )
| A. | 5个x相加 | B. | 5个x相乘 | C. | 6个x相加 | D. | 6个x相乘 |

 如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CD于E,AD=2.4cm,DE=1.7cm,则BE的长度为0.7cm.
如图,∠ACB=90°,AC=BC,AD⊥CE于D,BE⊥CD于E,AD=2.4cm,DE=1.7cm,则BE的长度为0.7cm.