题目内容
19.计算:$\frac{{\sqrt{27}+\sqrt{48}}}{{\sqrt{12}}}$-$\sqrt{\frac{1}{3}}•\sqrt{12}$.分析 先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算,在进行减法运算即可.
解答 解:原式=$\frac{3\sqrt{3}+4\sqrt{3}}{2\sqrt{3}}$-$\sqrt{\frac{1}{3}×12}$
=$\frac{7\sqrt{3}}{2\sqrt{3}}$-2
=$\frac{7}{2}$-2
=$\frac{3}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
17.已知一组数据x1,x2,…,xn的平均数是$\overline{x}$,方差为s2,则新的数据ax1+b,ax2+b,…,axn+b的平均数是a$\overline{x}$+b,方差是a2s2.
4.在同一直线上,线段AB=4cm,线段BC=3cm,则线段AC=( )
| A. | 7cm | B. | 12cm | C. | 1cm | D. | 7cm或1cm |
9.已$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$关于x、y的二元一次方程3x-ay=7的一个解,则a的值为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | --$\frac{1}{5}$ | D. | -5 |
 小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题:
小亮家最近买了一套住房,准备在装修时用木质地板铺设居室,用瓷砖铺设客厅,经市场调查得知,用这两种材料铺设地面的工钱不一样,小亮根据地面的面积,对铺设居室和客厅的费用(购买材料费和工钱)y分别作了预算,通过列表,并用x(㎡)表示铺设地面的面积,用y(元)表示铺设费用制成图.请你根据图4中所提供的信息,解答下列问题: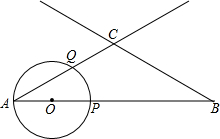 如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.
如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.