题目内容
如图,Rt△ABC中,∠BAC=90°,AB=AC,点D是BC上任意一点,过B作BE⊥AD于点E,过C作CF⊥AD于F.
(1)求证:BE-CF=EF;
(2)若D在BC的延长线上,如图(2),(1)中的结论还成立吗?若不成立,请写出新的结论并证明.

(1)求证:BE-CF=EF;
(2)若D在BC的延长线上,如图(2),(1)中的结论还成立吗?若不成立,请写出新的结论并证明.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)如图(1),证明△ABE≌△CAF,得到BE=AF,AE=CF,故EF=BE-CF.
(2)如图(2),证明△ABE≌△CAF,得到BE=AF,AE=CF,故EF=BE+CF.
(2)如图(2),证明△ABE≌△CAF,得到BE=AF,AE=CF,故EF=BE+CF.
解答: (1)证明:如图(1)
(1)证明:如图(1)
∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠ABE+∠BAE=∠BAE+∠FAC,
∴∠ABE=∠FAC;
在△ABE与△CAF中,
,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴EF=BE-CF.
(2)证明:如图(2),
∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠EBA+∠BAE=∠BAE+∠CAF,
∴∠EBA=∠CAF;
在△ABE与△CAF中,
,
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴EF=BE+CF.
 (1)证明:如图(1)
(1)证明:如图(1)∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠ABE+∠BAE=∠BAE+∠FAC,
∴∠ABE=∠FAC;
在△ABE与△CAF中,
|
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴EF=BE-CF.
(2)证明:如图(2),
∵∠BAC=90°,且BE⊥AD,CF⊥AD,
∴∠EBA+∠BAE=∠BAE+∠CAF,
∴∠EBA=∠CAF;
在△ABE与△CAF中,
|
∴△ABE≌△CAF(AAS),
∴BE=AF,AE=CF,
∴EF=BE+CF.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是深入观察图形结构特点,准确找出图形中隐含的相等或全等关系.

练习册系列答案
相关题目
 如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )
如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
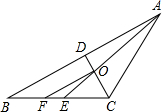 如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )
如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )A、∠OAB=
| ||
| B、∠OEC=∠OCE | ||
C、∠OAB=
| ||
| D、OC⊥OF | ||
| E、∠OEC=∠OCE |
若多边形的边数由3开始增加,则其外角和( )
| A、增加 | B、不变 |
| C、减少 | D、(n-2)×180° |
 如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.
如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x. 如图,△ABC是等边三角形,过它的三个顶点分别作为对边的平行线,得到一个新的△DEF,△DEF是等边三角形?你还能找到其他的等边三角形?点A、B、C分别是EF、ED、FD的中点吗?请证明你的结论.
如图,△ABC是等边三角形,过它的三个顶点分别作为对边的平行线,得到一个新的△DEF,△DEF是等边三角形?你还能找到其他的等边三角形?点A、B、C分别是EF、ED、FD的中点吗?请证明你的结论. 如图,在△ABC中,AD是BC边上的中线,AB=9,AD=6,AC=15,求△ABC的面积.
如图,在△ABC中,AD是BC边上的中线,AB=9,AD=6,AC=15,求△ABC的面积. 如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数.
如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数. 如图所示,P为平行四边形ABCD内一点,求证:以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.
如图所示,P为平行四边形ABCD内一点,求证:以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.