题目内容
 如图,在△ABC中,AD是BC边上的中线,AB=9,AD=6,AC=15,求△ABC的面积.
如图,在△ABC中,AD是BC边上的中线,AB=9,AD=6,AC=15,求△ABC的面积.考点:全等三角形的判定与性质,勾股定理的逆定理
专题:
分析:如图,作辅助线;证明△ABD≌△ECD,得到DE=AD=6,EC=AB=9;运用勾股定理证明∠AEC=90°,得到△AEC为直角三角形;求出△ACE的面积,即可解决问题.
解答: 解:如图,过点C作CE∥AB,交AD的延长线于点E;
解:如图,过点C作CE∥AB,交AD的延长线于点E;
则∠ABD=∠ECD;
在△ABD与△ECD中,
,
∴△ABD≌△ECD(ASA),
∴DE=AD=6,EC=AB=9;
∵AE2+EC2=122+92=225,
AC2=152=225,
∴AE2+EC2=AC2,
∴∠AEC=90°,S△AEC=
AE•EC=
×12×9=54;
∵△ABD≌△ECD,
∴S△ABD=S△DEC,
∴S△ABC=S△AEC=54.
 解:如图,过点C作CE∥AB,交AD的延长线于点E;
解:如图,过点C作CE∥AB,交AD的延长线于点E;则∠ABD=∠ECD;
在△ABD与△ECD中,
|
∴△ABD≌△ECD(ASA),
∴DE=AD=6,EC=AB=9;
∵AE2+EC2=122+92=225,
AC2=152=225,
∴AE2+EC2=AC2,
∴∠AEC=90°,S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABD≌△ECD,
∴S△ABD=S△DEC,
∴S△ABC=S△AEC=54.
点评:该题主要考查了全等三角形的判定和性质,勾股定理的逆定理,三角形的面积公式等知识点及其应用问题;解题的关键是作辅助线,构造全等三角形.

练习册系列答案
相关题目
中国是仅次于美国的世界第二大经济体.国家统计局发布的《2013年国民经济和社会发展统计公报》显示2013年我国国内生产总值为56.89万亿元,同比增长7.7%,56.89万亿元用科学记数法表示为( )
| A、5.689×106亿元 |
| B、0.5689×106亿元 |
| C、5.689×105亿元 |
| D、5689×102亿元 |
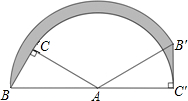 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至A′B′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至A′B′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长.
如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长. 如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n).
如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n). 如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.
如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.
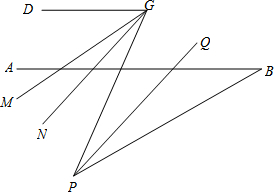 如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.