题目内容
 如图所示,P为平行四边形ABCD内一点,求证:以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.
如图所示,P为平行四边形ABCD内一点,求证:以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.考点:平行四边形的性质
专题:证明题
分析:过点B作AP的平行线BM,过点C作PD的平行线CM交BM于点PM,连接PPM,交BC于点M,可证明四边形ABMP为满足条件的四边形.
解答: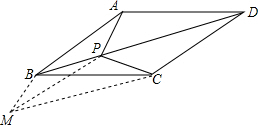 证明:过点B作AP的平行线BM,过点C作PD的平行线CM交BM于点PM,连接PPM,交BC于点M.
证明:过点B作AP的平行线BM,过点C作PD的平行线CM交BM于点PM,连接PPM,交BC于点M.
∵AP∥BM,PD∥CM,
∴∠PAB+∠ABM=180°,∠PDC+∠DCM=180°,
以BM、BP、PC、MC为边构成四边形,
则四边形ABMP为平行四边形,
∴BM=AP,同理可得MC=PD,
∴四边形BPCM为以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.
 证明:过点B作AP的平行线BM,过点C作PD的平行线CM交BM于点PM,连接PPM,交BC于点M.
证明:过点B作AP的平行线BM,过点C作PD的平行线CM交BM于点PM,连接PPM,交BC于点M.∵AP∥BM,PD∥CM,
∴∠PAB+∠ABM=180°,∠PDC+∠DCM=180°,
以BM、BP、PC、MC为边构成四边形,
则四边形ABMP为平行四边形,
∴BM=AP,同理可得MC=PD,
∴四边形BPCM为以AP、BP、CP、DP为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB和BC.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
相关题目

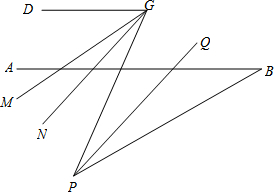 如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值.
如图,在(1)的结论下,AB的下方点P满足∠ABP=30°,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变.可以证明,只有一个是正确的,请你作出正确的选择并求值. 如图,等边△OAB的一边OA在x轴上,双曲线y=
如图,等边△OAB的一边OA在x轴上,双曲线y=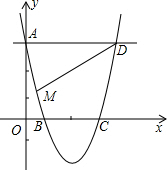 如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线.
如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线.