题目内容
 如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数.
如图,点O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠OAE的度数.考点:矩形的性质
专题:
分析:根据矩形的性质求出∠DAB=90°,OA=OB,得出等边三角形AOB,推出∠OAB=60°,求出∠BAE度数,即可得出答案.
解答:解:∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO,BD=2BO,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠OAB=60°,
∵∠DAB=90°,AE平分∠DAB,
∴∠BAE=45°,
∴∠OAE=∠OAB-∠BAE=60°-45°=15°.
∴∠DAB=90°,AC=2AO,BD=2BO,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠OAB=60°,
∵∠DAB=90°,AE平分∠DAB,
∴∠BAE=45°,
∴∠OAE=∠OAB-∠BAE=60°-45°=15°.
点评:本题考查了矩形的性质,等边三角形的性质和判定,角平分线定义的应用,解此题的关键是求出∠OAB和∠BAE度数,注意:矩形的对角线互相平分且相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在∠AOB的内部从顶点O引出3条射线,则图中共有角的个数是( )
在∠AOB的内部从顶点O引出3条射线,则图中共有角的个数是( )| A、9个 | B、10个 |
| C、11个 | D、12个 |
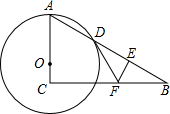 如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E.
如图,已知点O是Rt△ABC的直角边AC上的一动点,以O为圆心,OA为半径的⊙O交AB于D点,DB垂直平分线交BC于F,交BD于E. 如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长.
如图,△ABC中,BO、CO分别平分∠ABC和∠ACB,过点O平行于BC的直线分别交AB、AC于点D、E,已知AB=9cm,AC=8cm,求△ADE的周长. 如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.
如图所示,∠BAF,∠CBD,∠ACE是△ABC的三个外角,求∠BAF+∠CBD+∠ACE的度数.