题目内容
11.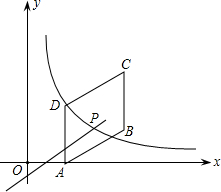 如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:①反比例函数的解析式是y1=$\frac{6}{x}$;
②一次函数y2=kx+3-3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3-3k的图象经过点C,当x$>2\sqrt{2}$时,y1<y2;
④对于一次函数y2=kx+3-3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是$\frac{a}{3}$<a<3.
其中正确的是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
分析 ①由B(6,2),C(6,6)得到BC⊥x轴,BC=4,根据平行四边形的性质得AD=BC=4,而A点坐标为(2,0),可得到点D的坐标为(2,4),然后把D(2,4)代入y=$\frac{m}{x}$即可得到m=8,从而可确定反比例函数的解析式;
②把x=6代入y=kx+3-3k(k≠0)得到y=3k+3,即可说明一次函数y=kx+3-3k(k≠0)的图象不一定过点C;
③由一次函数图象过点C可找出k的值,联立一次函数解析式与双曲线解析式得出关于x、y的方程组,解方程组找出点P的坐标,结合函数图象即可得出结论;
④由一次函数的单调性可得出k>0,结合一次函数必过点(3,3),而此时同横坐标的双曲线上的点的坐标为(3,$\frac{8}{3}$),由此可得出a<3,结合点P在第一象限可知$\frac{a}{3}$<a,由此可得出结论成立.结合①②③④即可得出结论.
解答 解:①∵四边形ABCD是平行四边形,
∴AD=BC,
∵B(6,2),C(6,6),
∴BC⊥x轴,AD=BC=4,
而A点坐标为(2,0),
∴点D的坐标为(2,4),
∵反比例函数y1=$\frac{m}{x}$(x>0)的函数图象经过点D(2,4),
∴4=$\frac{m}{2}$,
∴m=8,
∴反比例函数的解析式为y=$\frac{8}{x}$,①不正确;
②当x=6时,y=kx+3-3k=6k+3-3k=3k+3≠6,
∴一次函数y=kx+3-3k(k≠0)的图象不一定过点C,②不正确;
③∵一次函数y2=kx+3-3k的图象经过点C,
∴6=6k+3-3k,解得:k=1.
∴y2=x.
联立$\left\{\begin{array}{l}{y=x}\\{y=\frac{8}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2\sqrt{2}}\\{y=2\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2\sqrt{2}}\\{y=-2\sqrt{2}}\end{array}\right.$(舍去).
结合函数图象即可得出:
当x$>2\sqrt{2}$时,y1<y2,③成立;
④∵一次函数y2=kx+3-3k(k≠0),y随x的增大而增大,
∴k>0,
∴交点P在第一象限,
∴点P横坐标a的取值范围是$\frac{a}{3}$<a.
将x=3带入到反比例函数y=$\frac{8}{x}$中,得:y=$\frac{8}{3}$.
又∵一次函数y2=kx+3-3k(k≠0)恒过点(3,3),点(3,$\frac{8}{3}$)在(3,3)的下方,
即点P应该在点(3,$\frac{8}{3}$)的左方,
∴点P横坐标a的取值范围是a<3.
即④正确.
综上可知:③④正确,
故选D.
点评 本题考查了反比例函数与一次函数的交点问题、平行四边形的性质以及一次函数的性质,解题的关键是逐条分析四条结论的正确性.本题属于中档题,难度不大,再解决该题时,首先判断出①②结论不正确即可得知答案为D,不必再去分析③④.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 新学期开始,我校调查每一位学生的体重 | |
| B. | 调查某品牌电视机的使用寿命 | |
| C. | 调查我市中学生的近视率 | |
| D. | 调查长江中现有鱼的种类 |
| A. | a3+a2=2a6 | B. | (-2a3)2=4a6 | C. | a2•a3=a6 | D. | a6÷a3=a2 |
| A. | x$>\frac{1}{3}$ | B. | x≠$\frac{1}{3}$ | C. | x$≥\frac{1}{3}$ | D. | x≥0 |
| A. | 2x+x2=3x3 | B. | x6÷x2=x3 | C. | 2x•x2=2x2 | D. | (-x2)3=-x6 |
| A. | a3+a3=a6 | B. | (a2)3=a5 | C. | (a2+3)0=1 | D. | a6÷a3=a2 |
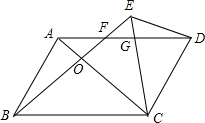 如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)
如图,?ABCD中,∠ABC=60°,F在AD边上,FD=AB,延长BF至点E,连接DE,连接CE交AD于点G,若∠BEC=60°,求证:CE=EF+DE.(要求:用四种不同方法证明,写出详细证明过程,并进行归纳总结)