题目内容
2.已知x=$\frac{2}{\sqrt{3}-1}$,求$\frac{1}{2}$x3-x2-x+1的值.分析 首先将x=$\frac{2}{\sqrt{3}-1}$进行分母有理化得到x=$\sqrt{3}+1$,然后将原式变形为$x(\frac{1}{2}{x}^{2}-x+1)+1$,接下来将x的值代入进行计算即可.
解答 解:x=$\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$=$\sqrt{3}+1$.
原式=$x(\frac{1}{2}{x}^{2}-x+1)+1$
=$(\sqrt{3}+1)(\frac{1}{2}(\sqrt{3}+1)^{2}-(\sqrt{3}+1)-1)+1$
=$(\sqrt{3}+1)[\frac{1}{2}(4+2\sqrt{3})-\sqrt{3}-1-1)+1$
=$(\sqrt{3}+1)(2+\sqrt{3}-\sqrt{3}-2)+1$
=$(\sqrt{3}+1)×0+1$
=1.
点评 本题主要考查的是二次根式的计算,将原式变形为$x(\frac{1}{2}{x}^{2}-x+1)+1$是解题的关键.

练习册系列答案
相关题目
 已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?
已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?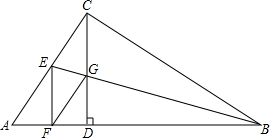 如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB.
如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB.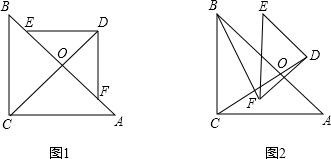
 如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.
如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由. 如图,△ABC是等腰直角三角形,点D是BC边的中点,点E,F分别在AC,BC上,连接DE,DF,∠EDF=90°.
如图,△ABC是等腰直角三角形,点D是BC边的中点,点E,F分别在AC,BC上,连接DE,DF,∠EDF=90°. 如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.